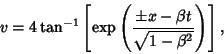| 释义 |
Sine-Gordon EquationA Partial Differential Equation which appears in differential geometry and relativistic field theory. Its name isa pun on its similar form to the Klein-Gordon Equation. The sine-Gordon equation is
 | (1) |
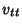 and and  are Partial Derivatives.The equation can be transformed by defining are Partial Derivatives.The equation can be transformed by defining
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 , ,
 | (6) |
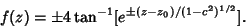 | (7) |
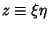 then gives then gives
 | (8) |
 gives gives
 | (9) |
 | (10) |
which can be solved in terms of Elliptic Functions. A single Soliton solution exists with  , , 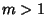 : :
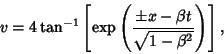 | (13) |
 | (14) |
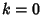 , , 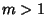 : :
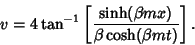 | (15) |
 , ,  , , 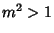 : :
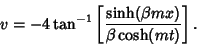 | (16) |
 | (17) |
References
Infeld, E. and Rowlands, G. Nonlinear Waves, Solitons, and Chaos. Cambridge, England: Cambridge University Press, pp. 199-200, 1990.
|