| 释义 |
Bauer's Identical CongruenceLet 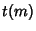 denote the set of the denote the set of the 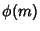 numbers less than and Relatively Prime to numbers less than and Relatively Prime to  , where , where  is theTotient Function. Define is theTotient Function. Define
 | (1) |
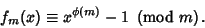 | (2) |
 be an Odd Prime Divisor of be an Odd Prime Divisor of  and and 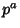 thehighest Power which divides thehighest Power which divides  , then , then
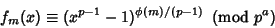 | (3) |
 | (4) |
 is Even and is Even and 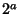 is the highest Power of 2 that divides is the highest Power of 2 that divides  , then , then
 | (5) |
 | (6) |
References
Hardy, G. H. and Wright, E. M. ``Bauer's Identical Congruence.'' §8.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 98-100, 1979.
|
![]() denote the set of the
denote the set of the ![]() numbers less than and Relatively Prime to
numbers less than and Relatively Prime to ![]() , where
, where ![]() is theTotient Function. Define
is theTotient Function. Define