| 释义 |
Bernoulli Inequality
 | (1) |
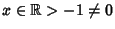 , , 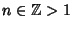 . This inequality can be proven by taking a Maclaurin Seriesof . This inequality can be proven by taking a Maclaurin Seriesof 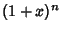 , ,
 | (2) |
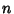 , the Bernoulli inequalityfor , the Bernoulli inequalityfor 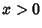 is obtained by truncating after the first-order term. When is obtained by truncating after the first-order term. When  , slightly more finesse is needed. In thiscase, let , slightly more finesse is needed. In thiscase, let 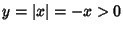 so that so that 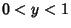 , and take , and take
 | (3) |
 multiplies by a number multiplies by a number  and since the Absolute Value of the Coefficient ofeach subsequent term is smaller than the last, it follows that the sum of the third order and subsequent terms is a Positivenumber. Therefore, and since the Absolute Value of the Coefficient ofeach subsequent term is smaller than the last, it follows that the sum of the third order and subsequent terms is a Positivenumber. Therefore,
 | (4) |
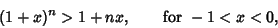 | (5) |
|