| 释义 |
Coin TossingAn idealized coin consists of a circular disk of zero thickness which, when thrown in the air and allowed to fall, willrest with either side face up (``heads'' H or ``tails'' T) with equal probability. A coin is therefore a two-sidedDie. A coin toss corresponds to a Bernoulli Distribution with  . Despite slightdifferences between the sides and Nonzero thickness of actual coins, the distribution of their tosses makes a goodapproximation to a . Despite slightdifferences between the sides and Nonzero thickness of actual coins, the distribution of their tosses makes a goodapproximation to a  Bernoulli Distribution. Bernoulli Distribution.
There are, however, some rather counterintuitive properties of coin tossing. For example, it is twice as likely that thetriple TTH will be encountered before THT than after it, and three times as likely that THH will precedeHTT. Furthermore, it is six times as likely that HTT will be the first of HTT, TTH, and TTTto occur (Honsberger 1979). More amazingly still, spinning a penny instead of tossing itresults in heads only about 30% of the time (Paulos 1995).
Let  be the probability that no Run of three consecutive heads appears in be the probability that no Run of three consecutive heads appears in  independent tosses of a Coin.The following table gives the first few values of independent tosses of a Coin.The following table gives the first few values of  . . Feller (1968, pp. 278-279) proved that
 | (1) |
and
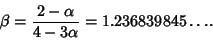 | (3) |
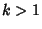 heads are heads are 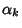 , the smallest Positive Root of , the smallest Positive Root of
 | (4) |
 | (5) |
 and and 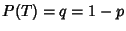 to to 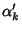 , the smallest Positive Root of , the smallest Positive Root of
 | (6) |
 | (7) |
References
Feller, W. An Introduction to Probability Theory and Its Application, Vol. 1, 3rd ed. New York: Wiley, 1968.Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/feller/feller.html Ford, J. ``How Random is a Coin Toss?'' Physics Today 36, 40-47, 1983. Honsberger, R. ``Some Surprises in Probability.'' Ch. 5 in Mathematical Plums (Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., pp. 100-103, 1979. Keller, J. B. ``The Probability of Heads.'' Amer. Math. Monthly 93, 191-197, 1986. Paulos, J. A. A Mathematician Reads the Newspaper. New York: BasicBooks, p. 75, 1995. Peterson, I. Islands of Truth: A Mathematical Mystery Cruise. New York: W. H. Freeman, pp. 238-239, 1990. Spencer, J. ``Combinatorics by Coin Flipping.'' Coll. Math. J., 17, 407-412, 1986.
|
![]() . Despite slightdifferences between the sides and Nonzero thickness of actual coins, the distribution of their tosses makes a goodapproximation to a
. Despite slightdifferences between the sides and Nonzero thickness of actual coins, the distribution of their tosses makes a goodapproximation to a ![]() Bernoulli Distribution.
Bernoulli Distribution.![]() be the probability that no Run of three consecutive heads appears in
be the probability that no Run of three consecutive heads appears in ![]() independent tosses of a Coin.The following table gives the first few values of
independent tosses of a Coin.The following table gives the first few values of ![]() .
.