| 释义 |
Nonlinear Least Squares FittingGiven a function 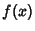 of a variable of a variable 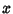 tabulated at tabulated at  values values 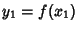 , ..., , ...,  , assume the function isof known analytic form depending on , assume the function isof known analytic form depending on  parameters parameters 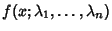 , and consider the overdetermined setof , and consider the overdetermined setof  equations equations
We desire to solve these equations to obtain the values 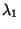 , ..., , ..., 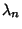 which best satisfy this systemof equations. Pick an initial guess for the which best satisfy this systemof equations. Pick an initial guess for the 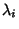 and then define and then define
 | (3) |
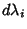 needed to reduce needed to reduce  to 0, to 0,
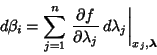 | (4) |
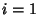 , ..., , ...,  . This can be written in component form as . This can be written in component form as
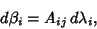 | (5) |
 is the is the  Matrix Matrix
 | (6) |
 | (7) |
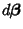 and and 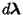 are are  -Vectors. Applying the Matrix Transpose of -Vectors. Applying the Matrix Transpose of  to bothsides gives to bothsides gives
 | (8) |
in terms of the known quantities  and and 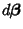 then gives the Matrix Equation then gives the Matrix Equation
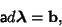 | (11) |
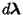 using standard matrix techniques such as Gaussian Elimination. This offset isthen applied to using standard matrix techniques such as Gaussian Elimination. This offset isthen applied to  and a new and a new 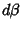 is calculated. By iteratively applying this procedure until the elements of is calculated. By iteratively applying this procedure until the elements of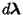 become smaller than some prescribed limit, a solution is obtained. Note that the procedure may not convergevery well for some functions and also that convergence is often greatly improved by picking initial values close to thebest-fit value. The sum of square residuals is given by become smaller than some prescribed limit, a solution is obtained. Note that the procedure may not convergevery well for some functions and also that convergence is often greatly improved by picking initial values close to thebest-fit value. The sum of square residuals is given by 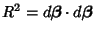 after the final iteration. after the final iteration.
An example of a nonlinear least squares fit to a noisy Gaussian Function
 | (12) |
 , the initialguess was (0.8, 15, 4), and the converged values are (1.03105, 20.1369, 4.86022), with , the initialguess was (0.8, 15, 4), and the converged values are (1.03105, 20.1369, 4.86022), with 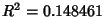 . The PartialDerivatives used to construct the matrix . The PartialDerivatives used to construct the matrix  are are
The technique could obviously be generalized to multiple Gaussians, to include slopes, etc., although theconvergence properties generally worsen as the number of free parameters is increased.
An analogous technique can be used to solve an overdetermined set of equations. This problem might, for example, arisewhen solving for the best-fit Euler Angles corresponding to a noisy Rotation Matrix, in which case there arethree unknown angles, but nine correlated matrix elements. In such a case, write the  different functions as different functions as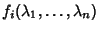 for for 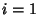 , ..., , ...,  , call their actual values , call their actual values 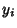 , and define , and define
 | (16) |
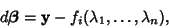 | (17) |
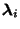 are the numerical values obtained after the are the numerical values obtained after the 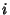 th iteration. Again, set up the equations as th iteration. Again, set up the equations as
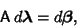 | (18) |
|
![]() of a variable
of a variable ![]() tabulated at
tabulated at ![]() values
values ![]() , ...,
, ..., ![]() , assume the function isof known analytic form depending on
, assume the function isof known analytic form depending on ![]() parameters
parameters ![]() , and consider the overdetermined setof
, and consider the overdetermined setof ![]() equations
equations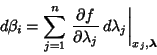



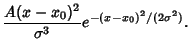
![]() different functions as
different functions as![]() for
for ![]() , ...,
, ..., ![]() , call their actual values
, call their actual values ![]() , and define
, and define