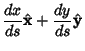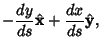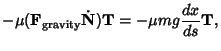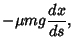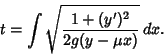| 释义 |
Brachistochrone ProblemFind the shape of the Curve down which a bead sliding from rest and Accelerated bygravity  will slip (without friction will slip (without friction  ) from one point to another in the leasttime. This was one of the earliest problems posed in the Calculus of Variations. The solution, a segment of aLeibniz, ) from one point to another in the leasttime. This was one of the earliest problems posed in the Calculus of Variations. The solution, a segment of aLeibniz,  L'Hospital, L'Hospital,  Newton, Newton,  and the twoBernoullis. and the twoBernoullis.
The time to travel from a point 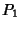 to another point to another point 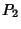 is given by the Integral is given by the Integral
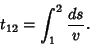 | (1) |
 equating kinetic energy equating kinetic energy  to gravitational potential energy, to gravitational potential energy, 
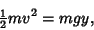 | (2) |
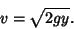 | (3) |
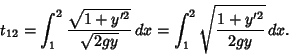 | (4) |
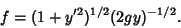 | (5) |
 | (6) |
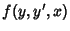 is particularly nice since is particularly nice since  does not appear explicitly. Therefore, does not appear explicitly. Therefore,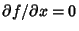 , and we can immediately use the Beltrami Identity , and we can immediately use the Beltrami Identity
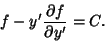 | (7) |
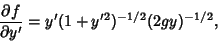 | (8) |
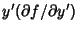 from from  , and simplifying then gives , and simplifying then gives
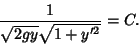 | (9) |
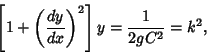 | (10) |
 has been expressed in terms of a new (Positive) constant has been expressed in terms of a new (Positive) constant 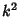 . This equation issolved by the parametric equations . This equation issolved by the parametric equations
which are--lo and behold--the equations of a Cycloid.
If kinetic friction  is included, the problem can also be solved analytically, although thesolution is significantly messier. In that case, terms corresponding to the normal component of weight is included, the problem can also be solved analytically, although thesolution is significantly messier. In that case, terms corresponding to the normal component of weight  and the normal component of the Acceleration (present because of path Curvature) must be included. Includingboth terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight onlygives an elementary solution. The Tangent and Normal Vectors are and the normal component of the Acceleration (present because of path Curvature) must be included. Includingboth terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight onlygives an elementary solution. The Tangent and Normal Vectors are
gravity  and friction and friction  are then are then
and the components along the curve are
so Newton's Second Law  gives gives
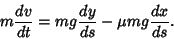 | (19) |
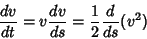 | (20) |
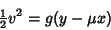 | (21) |
 | (22) |
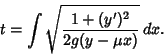 | (23) |
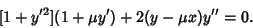 | (24) |
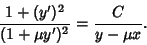 | (25) |
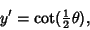 | (26) |
See also Cycloid, Tautochrone Problem
References
Ashby, N.; Brittin, W. E.; Love, W. F.; and Wyss, W. ``Brachistochrone with Coulomb Friction.'' Amer. J. Phys. 43, 902-905, 1975.Haws, L. and Kiser, T. ``Exploring the Brachistochrone Problem.'' Amer. Math. Monthly 102, 328-336, 1995. Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 60-66 and 385-389, 1991.
|
![]() will slip (without friction
will slip (without friction ![]() ) from one point to another in the leasttime. This was one of the earliest problems posed in the Calculus of Variations. The solution, a segment of aLeibniz,
) from one point to another in the leasttime. This was one of the earliest problems posed in the Calculus of Variations. The solution, a segment of aLeibniz, ![]() L'Hospital,
L'Hospital, ![]() Newton,
Newton, ![]() and the twoBernoullis.
and the twoBernoullis.![]() to another point
to another point ![]() is given by the Integral
is given by the Integral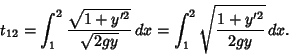
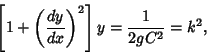
![]() is included, the problem can also be solved analytically, although thesolution is significantly messier. In that case, terms corresponding to the normal component of weight
is included, the problem can also be solved analytically, although thesolution is significantly messier. In that case, terms corresponding to the normal component of weight ![]() and the normal component of the Acceleration (present because of path Curvature) must be included. Includingboth terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight onlygives an elementary solution. The Tangent and Normal Vectors are
and the normal component of the Acceleration (present because of path Curvature) must be included. Includingboth terms requires a constrained variational technique (Ashby et al. 1975), but including the normal component of weight onlygives an elementary solution. The Tangent and Normal Vectors are