| 释义 |
SphereA sphere is defined as the set of all points in  which are a distance which are a distance 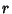 (the ``Radius'') from a givenpoint (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sidesof a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface ofa ``Bubble,'' which is denoted (the ``Radius'') from a givenpoint (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sidesof a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface ofa ``Bubble,'' which is denoted 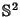 . However, in common usage, the word sphere is also used to mean theUnion of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. TheSurface Area of the sphere and Volume of the Ball of Radius . However, in common usage, the word sphere is also used to mean theUnion of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. TheSurface Area of the sphere and Volume of the Ball of Radius 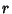 are given by are given by
(Beyer 1987, p. 130). In On the Sphere and Cylinder (ca. 225 BC  ), Archimedes ), Archimedes  became the first toderive these equations (although he expressed became the first toderive these equations (although he expressed 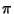 in terms of the sphere's circular cross-section). The fact that in terms of the sphere's circular cross-section). The fact that
 | (3) |

Any cross-section through a sphere is a Circle (or, in the degenerate case where the slicing Plane is tangent tothe sphere, a point). The size of the Circle is maximized when the Plane defining the cross-section passesthrough a Diameter.
The equation of a sphere of Radius 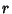 is given in Cartesian Coordinates by is given in Cartesian Coordinates by
 | (4) |
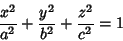 | (5) |
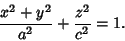 | (6) |
where 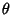 is an azimuthal coordinate running from 0 to is an azimuthal coordinate running from 0 to 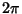 (Longitude), (Longitude),  is a polar coordinate runningfrom 0 to is a polar coordinate runningfrom 0 to 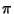 (Colatitude), and (Colatitude), and 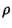 is the Radius. Note that there are several other notationssometimes used in which the symbols for is the Radius. Note that there are several other notationssometimes used in which the symbols for 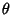 and and  are interchanged or where are interchanged or where 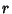 is used instead of is used instead of 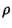 . If . If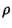 is allowed to run from 0 to a given Radius is allowed to run from 0 to a given Radius 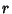 , then a solid Ball is obtained. Converting to ``standard'' parametric variables , then a solid Ball is obtained. Converting to ``standard'' parametric variables  , , 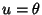 , and , and  gives the first FundamentalForms gives the first FundamentalForms
second Fundamental Forms
Area Element
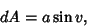 | (16) |
 | (17) |
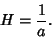 | (18) |
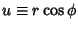 , so , so
where 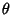 runs from 0 to runs from 0 to 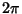 and and 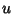 runs from runs from 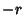 to to 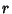 . .
Given two points on a sphere, the shortest path on the surface of the sphere which connects them (the Sphere Geodesic)is an Arc of a Circle known as a Great Circle. The equation of the sphere with points 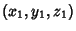 and and 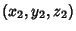 lying on a Diameter is given by lying on a Diameter is given by
 | (22) |
Four points are sufficient to uniquely define a sphere. Given the points 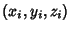 with with  , 2, 3, and 4, thesphere containing them is given by the beautiful Determinant equation , 2, 3, and 4, thesphere containing them is given by the beautiful Determinant equation
 | (23) |
The generalization of a sphere in 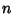 dimensions is called a Hypersphere. An dimensions is called a Hypersphere. An 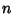 -D Hypersphere canbe specified by the equation -D Hypersphere canbe specified by the equation
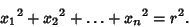 | (24) |
The distribution of Angles for random rotation of a sphere is
 | (25) |
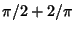 . .
To pick a random point on the surface of a sphere, let 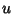 and and 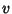 be random variates on be random variates on  . Then . Then
This works since the Solid Angle is
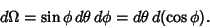 | (28) |
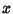 , , 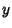 , and , and 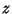 . Then the distribution of the vectors . Then the distribution of the vectors
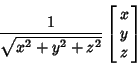 | (29) |
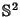 . Another method is to pick . Another method is to pick 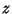 from a Uniform Distribution over from a Uniform Distribution over 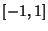 and and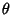 from a Uniform Distribution over from a Uniform Distribution over  . Then the points . Then the points
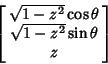 | (30) |
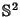 . .
Pick four points on a sphere. What is the probability that the Tetrahedron having these points asVertices contains the Center of the sphere? In the 1-D case, the probability that asecond point is on the opposite side of 1/2 is 1/2. In the 2-D case, pick two points. In order for the third to form aTriangle containing the Center, it must lie in the quadrant bisected by a Line Segment passing throughthe center of the Circle and the bisector of the two points. This happens for one Quadrant, so the probabilityis 1/4. Similarly, for a sphere the probability is one Octant, or 1/8.
Pick two points at random on a unit sphere. The first one can be assigned the coordinate (0, 0, 1) without loss ofgenerality. The second point can be given the coordinates 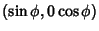 with with 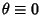 since all pointswith the same since all pointswith the same  are rotationally identical. The distance between the two points is then are rotationally identical. The distance between the two points is then
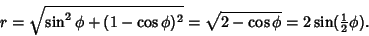 | (31) |
 | (32) |
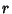 apart is apart is
The Delta Function contributes when
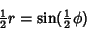 | (34) |
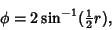 | (35) |
However, we need
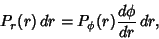 | (37) |
so
 | (39) |
 | (40) |
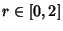 . Somewhat surprisingly, the largest distances are the most common, contrary to most people's intuition. Aplot of 15 random lines is shown below. . Somewhat surprisingly, the largest distances are the most common, contrary to most people's intuition. Aplot of 15 random lines is shown below.
The Moments about zero are
 | (41) |
Moments about the Mean are
so the Skewness and Kurtosis are
See also Ball, Bing's Theorem, Bubble, Circle, Dandelin Spheres, Diameter,Ellipsoid, Exotic Sphere, Fejes Tóth's Problem, Hypersphere,Liebmann's Theorem, Liouville's Sphere-Preserving Theorem, Mikusinski's Problem, Noise Sphere, Oblate Spheroid, Osculating Sphere, Parallelizable, ProlateSpheroid, Radius, Space Division, Sphere Packing, Tennis Ball Theorem
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.Eppstein, D. ``Circles and Spheres.''http://www.ics.uci.edu/~eppstein/junkyard/sphere.html. Geometry Center. ``The Sphere.'' http://www.geom.umn.edu/zoo/toptype/sphere/.
|
![]() which are a distance
which are a distance ![]() (the ``Radius'') from a givenpoint (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sidesof a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface ofa ``Bubble,'' which is denoted
(the ``Radius'') from a givenpoint (the ``Center''). Twice the Radius is called the Diameter, and pairs of points on opposite sidesof a Diameter are called Antipodes. The term ``sphere'' technically refers to the outer surface ofa ``Bubble,'' which is denoted ![]() . However, in common usage, the word sphere is also used to mean theUnion of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. TheSurface Area of the sphere and Volume of the Ball of Radius
. However, in common usage, the word sphere is also used to mean theUnion of a sphere and its Interior (a ``solid sphere''), where the Interior is called a Ball. TheSurface Area of the sphere and Volume of the Ball of Radius ![]() are given by
are given by![]() is given in Cartesian Coordinates by
is given in Cartesian Coordinates by![]() and
and ![]() lying on a Diameter is given by
lying on a Diameter is given by![]() with
with ![]() , 2, 3, and 4, thesphere containing them is given by the beautiful Determinant equation
, 2, 3, and 4, thesphere containing them is given by the beautiful Determinant equation
![]() dimensions is called a Hypersphere. An
dimensions is called a Hypersphere. An ![]() -D Hypersphere canbe specified by the equation
-D Hypersphere canbe specified by the equation![]() and
and ![]() be random variates on
be random variates on ![]() . Then
. Then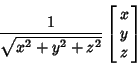
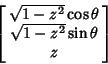
![]() with
with ![]() since all pointswith the same
since all pointswith the same ![]() are rotationally identical. The distance between the two points is then
are rotationally identical. The distance between the two points is then
