“Spherical Trigonometry”的概念、定义、习题解题方法及翻译-数学辞典

单词

Spherical Trigonometry

释义

Spherical Trigonometry

Define a Spherical Triangle on the surface of a unit Sphere, centered at a point , with vertices , ,and . Define Angles , , and . Let theAngle between Planes and be , the Angle between Planes and be , and the Angle between Planes and be . Define theVectors

			(1)
			(2)
			(3)

Then


			(4)

Equivalently,




			(5)

Since these two expressions are equal, we obtain the identity

(6)

The identity


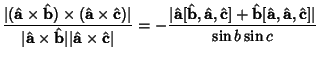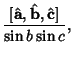			(7)

where

is the Scalar Triple Product, gives a spherical analog of the Law of Sines,

(8)

where

is the Volume of the Tetrahedron. From (7) and (8), it follows that

			(9)
			(10)

These are the fundamental equalities of spherical trigonometry.

There are also spherical analogs of the Law of Cosines for the sides of a spherical triangle,

			(11)
			(12)
			(13)

and the angles of a spherical triangle,

			(14)
			(15)
			(16)

(Beyer 1987), as well as the Law of Tangents

(17)

Let

			(18)
			(19)

then the half-angle formulas are

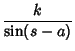			(20)
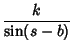			(21)
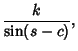			(22)

where

(23)

and the half-side formulas are

			(24)
			(25)
			(26)

where

(27)

where

is the Radius of the Sphere on which the spherical triangle lies.

Additional formulas include the Haversine formulas

			(28)
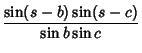			(29)
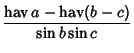			(30)
			(31)

Gauss's Formulas

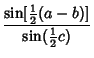			(32)
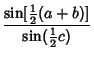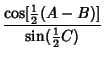			(33)
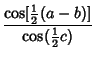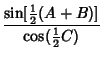			(34)
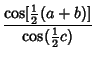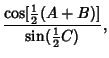			(35)

and Napier's Analogies

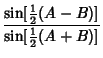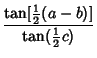			(36)
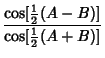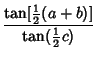			(37)
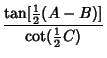			(38)
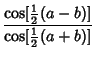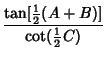			(39)

(Beyer 1987).

See also Angular Defect, Descartes Total Angular Defect, Gauss's Formulas, Girard's Spherical ExcessFormula, Law of Cosines, Law of Sines, Law of Tangents, L'Huilier's Theorem, Napier'sAnalogies, Spherical Excess, Spherical Geometry, Spherical Polygon, Spherical Triangle
References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 131 and 147-150, 1987.

Danby, J. M. Fundamentals of Celestial Mechanics, 2nd ed., rev. ed. Richmond, VA: Willmann-Bell, 1988.

Smart, W. M. Text-Book on Spherical Astronomy, 6th ed. Cambridge, England: Cambridge University Press, 1960.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。