| 释义 |
Trigonometry Values Pi/11Trigonometric functions of  for for 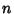 an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 11 is not a Fermat Prime. This also means that the Undecagon is nota Constructible Polygon. an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 11 is not a Fermat Prime. This also means that the Undecagon is nota Constructible Polygon.
However, exact expressions involving roots of complex numbers can still be derived using the trigonometric identity  | |  | (1) |
Using the identities from Beyer (1987, p. 139),
 | (2) |
 | (3) |
 and and 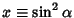 , then , then
 | (5) |
 , 0.29229, 0.57115, 0.82743, 0.97974. So , 0.29229, 0.57115, 0.82743, 0.97974. So , ,  , ,  , ,  , , 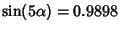 . Fromone of Newton's Identities,The trigonometric functions of . Fromone of Newton's Identities,The trigonometric functions of  also obey the identity also obey the identity
 | (9) |
References
Beyer, W. H. ``Trigonometry.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.
|
![]() for
for ![]() an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 11 is not a Fermat Prime. This also means that the Undecagon is nota Constructible Polygon.
an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 11 is not a Fermat Prime. This also means that the Undecagon is nota Constructible Polygon.