Prime Constellation
A prime constellation, also called a Prime k-Tuple or Prime k-Tuplet, is a sequence of ![]() consecutivenumbers such that the difference between the first and last is, in some sense, the least possible. More precisely, aprime
consecutivenumbers such that the difference between the first and last is, in some sense, the least possible. More precisely, aprime ![]() -tuplet is a sequence of consecutive Primes (
-tuplet is a sequence of consecutive Primes (![]() ,
, ![]() , ...,
, ..., ![]() ) with
) with ![]() , where
, where ![]() is the smallest number
is the smallest number ![]() for which there exist
for which there exist ![]() integers
integers ![]() ,
, ![]() and, for everyPrime
and, for everyPrime ![]() , not all the residues modulo
, not all the residues modulo ![]() are represented by
are represented by ![]() ,
, ![]() , ...,
, ..., ![]() (Forbes). For each
(Forbes). For each ![]() , thisdefinition excludes a finite number of clusters at the beginning of the prime number sequence. For example, (97, 101,103, 107, 109) satisfies the conditions of the definition of a prime 5-tuplet, but (3, 5, 7, 11, 13) does not becauseall three residues modulo 3 are represented (Forbes).
, thisdefinition excludes a finite number of clusters at the beginning of the prime number sequence. For example, (97, 101,103, 107, 109) satisfies the conditions of the definition of a prime 5-tuplet, but (3, 5, 7, 11, 13) does not becauseall three residues modulo 3 are represented (Forbes).
A prime double with ![]() is of the form (
is of the form (![]() ,
, ![]() ) and is called a pair of Twin Primes. Prime doubles of the form(
) and is called a pair of Twin Primes. Prime doubles of the form(![]() ,
, ![]() ) are called Sexy Primes. A prime triplet has
) are called Sexy Primes. A prime triplet has ![]() . The constellation (
. The constellation (![]() ,
, ![]() ,
, ![]() ) cannot exist,except for
) cannot exist,except for ![]() , since one of
, since one of ![]() ,
, ![]() , and
, and ![]() must be divisible by three. However, there are several types of primetriplets which can exist: (
must be divisible by three. However, there are several types of primetriplets which can exist: (![]() ,
, ![]() ,
, ![]() ), (
), (![]() ,
, ![]() ,
, ![]() ), (
), (![]() ,
, ![]() ,
, ![]() ). A Prime Quadruplet is aconstellation of four successive Primes with minimal distance
). A Prime Quadruplet is aconstellation of four successive Primes with minimal distance ![]() , and is of the form (
, and is of the form (![]() ,
, ![]() ,
, ![]() ,
, ![]() ). The sequence
). The sequence ![]() therefore begins 2, 6, 8, and continues 12, 16, 20, 26, 30, ... (Sloane's A008407). Another quadrupletconstellation is (
therefore begins 2, 6, 8, and continues 12, 16, 20, 26, 30, ... (Sloane's A008407). Another quadrupletconstellation is (![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
The first First Hardy-Littlewood Conjecture states that the numbers ofconstellations ![]() are asymptotically given by
are asymptotically given by
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) | |
| (6) | |
| (7) |
| (8) |
The integrals above have the analytic forms
 | (9) | ||
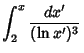 | 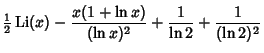 | (10) | |
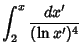 | 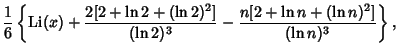 | (11) |
where
The following table gives the number of prime constellations ![]() , and the second table gives the valuespredicted by the Hardy-Littlewood formulas.
, and the second table gives the valuespredicted by the Hardy-Littlewood formulas.
| Count | ||||
| 1224 | 8169 | 58980 | 440312 | |
| 1216 | 8144 | 58622 | 440258 | |
| 2447 | 16386 | 117207 | 879908 | |
| 259 | 1393 | 8543 | 55600 | |
| 248 | 1444 | 8677 | 55556 | |
| 38 | 166 | 899 | 4768 | |
| 75 | 325 | 1695 | 9330 |
| Hardy-Littlewood | ||||
| 1249 | 8248 | 58754 | 440368 | |
| 1249 | 8248 | 58754 | 440368 | |
| 2497 | 16496 | 117508 | 880736 | |
| 279 | 1446 | 8591 | 55491 | |
| 279 | 1446 | 8591 | 55491 | |
| 53 | 184 | 863 | 4735 | |
Consider prime constellations in which each term is of the form ![]() . Hardy and Littlewood showed that the numberof prime constellations of this form
. Hardy and Littlewood showed that the numberof prime constellations of this form ![]() is given by
is given by
| (12) |
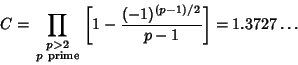 | (13) |
Forbes gives a list of the ``top ten'' prime ![]() -tuples for
-tuples for ![]() . The largest known 14-constellations are(
. The largest known 14-constellations are(![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(![]() , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50),(![]() , 2, 6, 8, 12, 18, 20, 26, 30, 32, 36, 42, 48, 50).
, 2, 6, 8, 12, 18, 20, 26, 30, 32, 36, 42, 48, 50).
The largest known prime 15-constellations are(![]() , 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56),(
, 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56),(![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),(![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),(![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56),(![]() , 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56).
, 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56).
The largest known prime 16-constellations are(![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),(![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),(
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60),(![]() , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73).
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73).
The largest known prime 17-constellations are
(![]() , 6, 8, 12, 18, 20, 26, 32, 36, 38, 42, 48, 50, 56, 60, 62, 66),(17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83)(13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79).
, 6, 8, 12, 18, 20, 26, 32, 36, 38, 42, 48, 50, 56, 60, 62, 66),(17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83)(13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79).
References
Forbes, T. ``Prime Guy, R. K. ``Patterns of Primes.'' §A9 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 23-25, 1994. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 38, 1983. Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 60-74, 1994. Sloane, N. J. A. Sequence A008407in ``The On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html.![]() -tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.
-tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.
- Reuleaux Triangle
- Reversal
- Reverse Greedy Algorithm
- Reverse-Then-Add Sequence
- Reversion of Series
- Reznik's Identity
- Rhodonea
- Rhomb
- Rhombic Dodecahedral Number
- Rhombic Dodecahedron
- Rhombic Icosahedron
- Rhombicosacron
- Rhombicosahedron
- Rhombicosidodecahedron
- Rhombic Polyhedron
- Rhombic Triacontahedron
- Rhombicuboctahedron
- Rhombidodecadodecahedron
- Rhombihexacron
- Rhombihexahedron
- Rhombitruncated Cuboctahedron
- Rhombitruncated Icosidodecahedron
- Rhombohedron
- Rhomboid
- Rhomboidal Dodecahedron