Cantor Set
The Cantor set (
) is given by taking the interval [0,1] (set 
), removing the middle third (
), removingthe middle third of each of the two remaining pieces (
), and continuing this procedure ad infinitum. It is thereforethe set of points in the Interval [0,1] whose ternary expansions do not contain 1,illustrated below.
This produces the Set of Real Numbers 
such that
 | (1) |
may equal 0 or 2 for each 
. This is an infinite, Perfect Set. The total length of the LineSegments in the th iteration is | (2) |
, so the length of each element is | (3) |
 |  |  | |
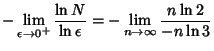 |  | (4) |
The Cantor set is nowhere Dense, so it has Lebesgue Measure 0.
A general Cantor set is a Closed Set consisting entirely of Boundary Points. Such setsare Uncountable and may have 0 or Positive Lebesgue Measure. The Cantor set is the only totallydisconnected, perfect, Compact Metric Space up to a Homeomorphism (Willard 1970).
See also Alexander's Horned Sphere, Antoine's Necklace, Cantor Function
References
Boas, R. P. Jr. A Primer of Real Functions. Washington, DC: Amer. Math. Soc., 1996. Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 15-20, 1991. Willard, S. §30.4 in General Topology. Reading, MA: Addison-Wesley, 1970.
- Homeomorphic Type
- Homeomorphism
- Home Plate
- HOMFLY Polynomial
- Homoclinic Point
- Homogeneous Coordinates
- Homogeneous Function
- Homogeneous Numbers
- Homogeneous Polynomial
- Homographic
- Homography
- Homological Algebra
- Homologous Points
- Homolographic Equal Area Projection
- Homology (Geometry)
- Homology Group
- Homology (Topology)
- Homomorphic
- Homomorphism
- Homoscedastic
- Homothecy
- Homothetic
- Homothetic Center
- Homothetic Position
- Homothetic Triangles