“Steiner Points”的概念、定义、习题解题方法及翻译-数学辞典

单词

Steiner Points

释义

Steiner Points

There are two different types of points known as Steiner points.

The point of Concurrence of the three lines drawn through the Vertices ofa Triangle Parallel to the corresponding sides of the first Brocard Triangle. Itlies on the Circumcircle opposite the Tarry Point and has Triangle Center Function

The Brianchon Point for Kiepert's Parabola is the Steiner point. The Lemoine Point

is theSteiner point of the first Brocard Triangle. The Simson Line of the Steinerpoint is Parallel to the line

, when

is the Circumcenter and

is the Lemoine Point.

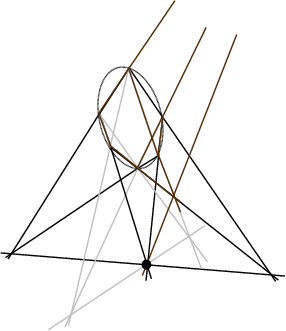
If triplets of opposites sides on a Conic Section in Pascal's Theorem are extended for all permutations ofVertices, 60 Pascal Lines are produced. The 20 points of their 3 by 3intersections are called Steiner points.

See also Brianchon Point, Brocard Triangles, Circumcircle, Conic Section, Kiepert's Parabola,Lemoine Point, Pascal Line, Pascal's Theorem, Steiner Set, Steiner Triple System,Tarry Point

References

Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., p. 66, 1893.

Gallatly, W. The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, p. 102, 1913.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 281-282, 1929.

Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。