Star Polygon

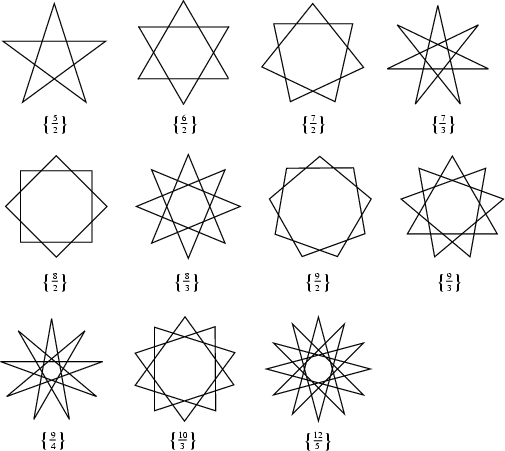
A star polygon , with Positive Integers, is a figure formed by connecting with straightlines every th point out of regularly spaced points lying on a Circumference. The number is called theDensity of the star polygon. Without loss of generality, take .

The usual definition (Coxeter 1969) requires and to be Relatively Prime. However, the starpolygon can also be generalized to the Star Figure (or ``improper'' star polygon) when and sharea common divisor (Savio and Suryanaroyan 1993). For such a figure, if all points are not connected after thefirst pass, i.e., if , then start with the first unconnected point and repeat the procedure. Repeat until all points are connected. For , the symbol can be factored as

(1)

			(2)
			(3)

If , a Regular Polygon is obtained. Special cases of include (the Pentagram), (the Hexagram, or Star of David), (the Star of Lakshmi), (theOctagram), (the Decagram), and (the Dodecagram).

The star polygons were first systematically studied by Thomas Bradwardine.

References

Coxeter, H. S. M. ``Star Polygons.'' §2.8 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 36-38, 1969.

Frederickson, G. ``Stardom.'' Ch. 16 in Dissections: Plane and Fancy. New York: Cambridge University Press, pp. 172-186, 1997.

Savio, D. Y. and Suryanaroyan, E. R. ``Chebyshev Polynomials and Regular Polygons.'' Amer. Math. Monthly 100, 657-661, 1993.

• Cayley's Ruled Surface
• Cayley's Sextic
• Cayley's Sextic Evolute
• Cayley Tree
• C-Curve
• C-Determinant
• Cech Cohomology
• Ceiling Function
• Cell
• Cellular Automaton
• Cellular Space
• Center
• Centered Cube Number
• Centered Hexagonal Number
• Centered Pentagonal Number
• Centered Polygonal Number
• Centered Square Number
• Centered Triangular Number
• Center Function
• Center (Group)
• Center of Gravity
• Center of Mass
• Centillion
• Central Angle
• Central Beta Function