| 释义 |
RunA run is a sequence of more than one consecutive identical outcomes, also known as a Clump. Given 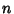 Bernoulli Trials (say, in theform of Coin Tossings), the probability Bernoulli Trials (say, in theform of Coin Tossings), the probability 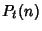 of a run of of a run of 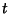 consecutive heads or tails is given by the Recurrence Relation consecutive heads or tails is given by the Recurrence Relation
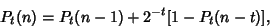 | (1) |
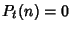 for for 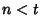 and and 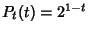 (Bloom 1996). (Bloom 1996).
Let  denote the number of sequences of denote the number of sequences of 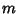 indistinguishable objects of type indistinguishable objects of type 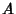 and and  indistinguishableobjects of type indistinguishableobjects of type 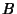 in which no in which no 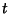 -run occurs. The probability that a -run occurs. The probability that a 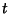 -run does occur is then givenby -run does occur is then givenby
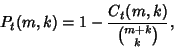 | (2) |
 is a Binomial Coefficient. Bloom (1996) gives the following recurrence sequence for is a Binomial Coefficient. Bloom (1996) gives the following recurrence sequence for , ,
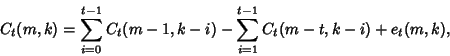 | (3) |
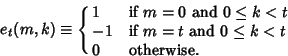 | (4) |
 | |  | (5) |
where
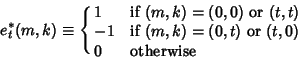 | (6) |
 . .
Given 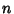 Bernoulli Trials with a probability of success (heads) Bernoulli Trials with a probability of success (heads)  , the expected number of tails is , the expected number of tails is  , so the expected number of tail runs , so the expected number of tail runs 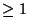 is is 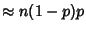 . Continuing, . Continuing,
 | (7) |
 . The longest expected run is therefore given by . The longest expected run is therefore given by
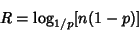 | (8) |
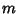 0s and 0s and 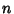 1s, the number of possible arrangements with 1s, the number of possible arrangements with  runs is runs is
 | (9) |
 an Integer, where an Integer, where 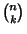 is a Binomial Coefficient. Then is a Binomial Coefficient. Then
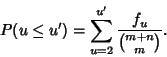 | (10) |
Bloom (1996) gives the expected number of noncontiguous 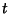 -runs in a sequence of -runs in a sequence of 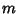 0sand 0sand 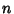 1s as 1s as
 | (11) |
 is the Pochhammer Symbol. For is the Pochhammer Symbol. For  , ,  has an approximately Normal Distribution withMean and Variance has an approximately Normal Distribution withMean and Variance
See also Coin Tossing, Eulerian Number, Permutation, s-Run
References
Bloom, D. M. ``Probabilities of Clumps in a Binary Sequence (and How to Evaluate Them Without Knowing a Lot).'' Math. Mag. 69, 366-372, 1996.Gardner, M. Aha! Gotcha: Paradoxes to Puzzle and Delight. New York: W. H. Freeman, p. 124, 1982. Godbole, A. P. ``On Hypergeometric and Related Distributions of Order  .'' Commun. Stat.: Th. and Meth. 19, 1291-1301, 1990. .'' Commun. Stat.: Th. and Meth. 19, 1291-1301, 1990. Godbole, A. P. and Papastavnidis, G. (Eds.). Runs and Patterns in Probability: Selected Papers. New York: Kluwer, 1994. Gordon, L.; Schilling, M. F.; and Waterman, M. S. ``An Extreme Value Theory for Long Head Runs.'' Prob. Th. and Related Fields 72, 279-287, 1986. Goulden, I. P. and Jackson, D. M. Combinatorial Enumeration. New York: Wiley, 1983. Mood, A. M. ``The Distribution Theory of Runs.'' Ann. Math. Statistics 11, 367-392, 1940. Philippou, A. N. and Makri, F. S. ``Successes, Runs, and Longest Runs.'' Stat. Prob. Let. 4, 211-215, 1986. Schilling, M. F. ``The Longest Run of Heads.'' Coll. Math. J. 21, 196-207, 1990. Schuster, E. F. In Runs and Patterns in Probability: Selected Papers (Ed. A. P. Godbole and S. Papastavridis). Boston, MA: Kluwer, pp. 91-111, 1994. |
![]() Bernoulli Trials (say, in theform of Coin Tossings), the probability
Bernoulli Trials (say, in theform of Coin Tossings), the probability ![]() of a run of
of a run of ![]() consecutive heads or tails is given by the Recurrence Relation
consecutive heads or tails is given by the Recurrence Relation![]() denote the number of sequences of
denote the number of sequences of ![]() indistinguishable objects of type
indistinguishable objects of type ![]() and
and ![]() indistinguishableobjects of type
indistinguishableobjects of type ![]() in which no
in which no ![]() -run occurs. The probability that a
-run occurs. The probability that a ![]() -run does occur is then givenby
-run does occur is then givenby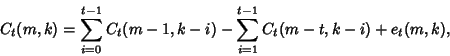
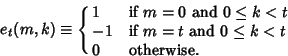
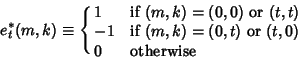
![]() Bernoulli Trials with a probability of success (heads)
Bernoulli Trials with a probability of success (heads) ![]() , the expected number of tails is
, the expected number of tails is ![]() , so the expected number of tail runs
, so the expected number of tail runs ![]() is
is ![]() . Continuing,
. Continuing,
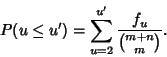
![]() -runs in a sequence of
-runs in a sequence of ![]() 0sand
0sand ![]() 1s as
1s as
![]() .'' Commun. Stat.: Th. and Meth. 19, 1291-1301, 1990.
.'' Commun. Stat.: Th. and Meth. 19, 1291-1301, 1990.