| 释义 |
Stokes' TheoremFor  a Differential k-Form with compact support on an oriented a Differential k-Form with compact support on an oriented  -dimensional Manifold -dimensional Manifold 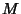 , ,
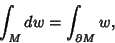 | (1) |
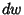 is the Exterior Derivative of the differential form is the Exterior Derivative of the differential form  . This connects to the ``standard''Gradient, Curl, and Divergence Theoremsby the following relations. If . This connects to the ``standard''Gradient, Curl, and Divergence Theoremsby the following relations. If 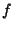 is a function on is a function on 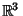 , ,
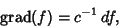 | (2) |
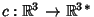 (the dual space) is the duality isomorphism between a Vector Spaceand its dual, given by the Euclidean Inner Product on (the dual space) is the duality isomorphism between a Vector Spaceand its dual, given by the Euclidean Inner Product on 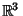 . If . If 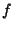 is a Vector Field on a is a Vector Field on a 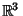 , ,
 | (3) |
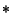 is the Hodge Star operator. If is the Hodge Star operator. If 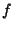 is a Vector Field on is a Vector Field on 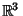 , ,
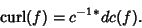 | (4) |
With these three identities in mind, the above Stokes' theorem in the three instances is transformed into theGradient, Curl, and Divergence Theoremsrespectively as follows. If 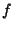 is a function on is a function on 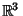 and and 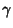 is a curve in is a curve in 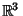 , then , then
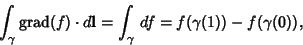 | (5) |
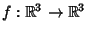 is a Vector Field and is a Vector Field and 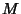 an embedded compact3-manifold with boundary in an embedded compact3-manifold with boundary in 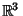 , then , then
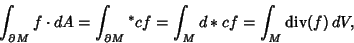 | (6) |
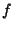 is a Vector Field and is a Vector Field and 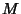 is an oriented, embedded, compact 2-Manifold with boundary in is an oriented, embedded, compact 2-Manifold with boundary in 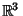 , then , then
 | (7) |
Physicists generally refer to the Curl Theorem
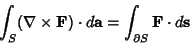 | (8) |
|
![]() a Differential k-Form with compact support on an oriented
a Differential k-Form with compact support on an oriented ![]() -dimensional Manifold
-dimensional Manifold ![]() ,
,![]() is a function on
is a function on ![]() and
and ![]() is a curve in
is a curve in ![]() , then
, then