| 释义 |
Student's t-DistributionA Distribution published by William Gosset in 1908. His employer, Guinness Breweries, required him to publish under apseudonym, so he chose ``Student.'' Given  independent measurements independent measurements  , let , let
 | (1) |
 is the population Mean, is the population Mean,  is the sample Mean, and is the sample Mean, and  is the Estimator for population Standard Deviation (i.e., the Sample Variance) defined by is the Estimator for population Standard Deviation (i.e., the Sample Variance) defined by
 | (2) |
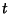 -distribution is defined as the distribution of the random variable -distribution is defined as the distribution of the random variable 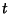 which is (very loosely) the ``best''that we can do not knowing which is (very loosely) the ``best''that we can do not knowing 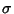 . If . If  , ,  and the distribution becomes the Normal Distribution. As and the distribution becomes the Normal Distribution. As increases, Student's increases, Student's 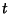 -distribution approaches the Normal Distribution. -distribution approaches the Normal Distribution.
Student's 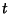 -distribution is arrived at by transforming to Student's z-Distribution with -distribution is arrived at by transforming to Student's z-Distribution with
 | (3) |
 | (4) |
where
 | (7) |
 , ,  is the Gamma Function, is the Gamma Function, is the Beta Function, and is the Beta Function, and  is the Regularized Beta Function defined by is the Regularized Beta Function defined by
 | (8) |
The Mean, Variance, Skewness, and Kurtosis of Student's 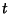 -distribution are -distribution are
Beyer (1987, p. 514) gives 60%, 70%, 90%, 95%, 97.5%, 99%, 99.5%, and 99.95% confidence intervals, and Goulden (1956) gives 50%, 90%, 95%, 98%, 99%, and 99.9% confidence intervals. A partial table is givenbelow for small  and several common confidence intervals. and several common confidence intervals.  | 80% | 90% | 95% | 99% | | 1 | 3.08 | 6.31 | 12.71 | 63.66 | | 2 | 1.89 | 2.92 | 4.30 | 9.92 | | 3 | 1.64 | 2.35 | 3.18 | 5.84 | | 4 | 1.53 | 2.13 | 2.78 | 4.60 | | 5 | 1.48 | 2.01 | 2.57 | 4.03 | | 10 | 1.37 | 1.81 | 2.23 | 4.14 | | 30 | 1.31 | 1.70 | 2.04 | 2.75 | | 100 | 1.29 | 1.66 | 1.98 | 2.63 | 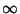 | 1.28 | 1.65 | 1.96 | 2.58 |
The so-called  distribution is useful for testing if two observed distributions have the same Mean. distribution is useful for testing if two observed distributions have the same Mean.  gives the probability that the difference in two observed Means for a certain statistic gives the probability that the difference in two observed Means for a certain statistic 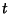 with with  Degrees of Freedom would be smaller than the observed value purely by chance: Degrees of Freedom would be smaller than the observed value purely by chance:
 | (13) |
 be a Normally Distributed random variable with Mean 0 and Variance be a Normally Distributed random variable with Mean 0 and Variance , let , let  have a Chi-Squared Distribution with have a Chi-Squared Distribution with  Degrees of Freedom, and let Degrees of Freedom, and let  and and 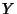 be independent. Then be independent. Then
 | (14) |
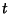 with with  Degrees of Freedom. Degrees of Freedom.
The noncentral Student's 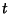 -distribution is given by -distribution is given by
where  is the Gamma Function, is the Gamma Function,  is a Confluent Hypergeometric Function,and is a Confluent Hypergeometric Function,and  is an associated Laguerre Polynomial. is an associated Laguerre Polynomial. See also Paired t-Test, Student's z-Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 948-949, 1972.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 536, 1987. Fisher, R. A. ``Applications of `Student's' Distribution.'' Metron 5, 3-17, 1925. Fisher, R. A. ``Expansion of `Student's' Integral in Powers of  .'' Metron 5, 22-32, 1925. .'' Metron 5, 22-32, 1925. Fisher, R. A. Statistical Methods for Research Workers, 10th ed. Edinburgh: Oliver and Boyd, 1948. Goulden, C. H. Table A-3 in Methods of Statistical Analysis, 2nd ed. New York: Wiley, p. 443, 1956. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution.'' §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 219-223, 1992. Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 116-117, 1992. Student. ``The Probable Error of a Mean.'' Biometrika 6, 1-25, 1908.
|

![]() independent measurements
independent measurements ![]() , let
, let
![]() -distribution is arrived at by transforming to Student's z-Distribution with
-distribution is arrived at by transforming to Student's z-Distribution with





![]() -distribution are
-distribution are![]() and several common confidence intervals.
and several common confidence intervals.![]() distribution is useful for testing if two observed distributions have the same Mean.
distribution is useful for testing if two observed distributions have the same Mean. ![]() gives the probability that the difference in two observed Means for a certain statistic
gives the probability that the difference in two observed Means for a certain statistic ![]() with
with ![]() Degrees of Freedom would be smaller than the observed value purely by chance:
Degrees of Freedom would be smaller than the observed value purely by chance:
![]() -distribution is given by
-distribution is given by


![]() is the Gamma Function,
is the Gamma Function, ![]() is a Confluent Hypergeometric Function,and
is a Confluent Hypergeometric Function,and ![]() is an associated Laguerre Polynomial.
is an associated Laguerre Polynomial.![]() .'' Metron 5, 22-32, 1925.
.'' Metron 5, 22-32, 1925.