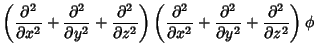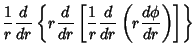| 释义 |
Biharmonic EquationThe differential equation obtained by applying the Biharmonic Operator and setting to zero.
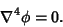 | (1) |
In Polar Coordinates (Kaplan 1984, p. 148)
For a radial function 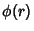 , the biharmonic equation becomes , the biharmonic equation becomes
Writing the inhomogeneous equation as
 | (5) |
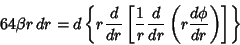 | (6) |
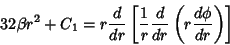 | (7) |
 | (8) |
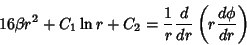 | (9) |
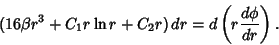 | (10) |
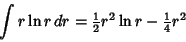 | (11) |
 | (12) |
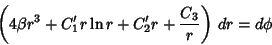 | (13) |
The homogeneous biharmonic equation can be separated and solved in 2-D Bipolar Coordinates.
References
Kaplan, W. Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, 1991.
|