| 释义 |
CircumradiusThe radius of a Triangle's Circumcircle or of a Polyhedron's Circumsphere, denoted  . For a Triangle, . For a Triangle,
 | (1) |
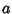 , ,  , and , and 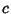 . .
This equation can also be expressed in terms of the Radii of the three mutually tangentCircles centered at the Triangle's Vertices. Relabeling the diagram forthe Soddy Circles with Vertices 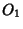 , ,  , and , and 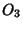 and the radii and the radii 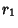 , ,  , and , and , and using , and using
then gives
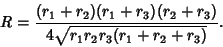 | (5) |
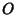 is the Circumcenter and is the Circumcenter and  is the triangle Centroid, then is the triangle Centroid, then
 | (6) |
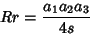 | (7) |
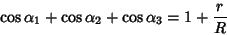 | (8) |
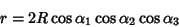 | (9) |
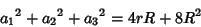 | (10) |
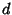 be the distance between Inradius be the distance between Inradius  and circumradius and circumradius  , , . Then . Then
 | (11) |
 | (12) |
For an Archimedean Solid, expressing the circumradius in terms of the Inradius  and Midradius and Midradius gives gives
for an Archimedean Solid.See also Carnot's Theorem, Circumcircle, Circumsphere
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929.Mackay, J. S. ``Historical Notes on a Geometrical Theorem and its Developments [18th Century].'' Proc. Edinburgh Math. Soc. 5, 62-78, 1886-1887.
|
![]() . For a Triangle,
. For a Triangle,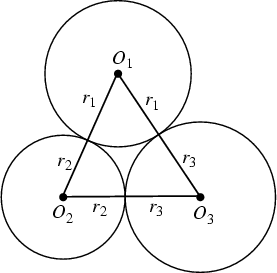
![]() ,
, ![]() , and
, and ![]() and the radii
and the radii ![]() ,
, ![]() , and
, and![]() , and using
, and using![]() and Midradius
and Midradius![]() gives
gives