| 释义 |
Collatz ProblemA problem posed by L. Collatz in 1937, also called the 3x+1 Mapping, Hasse's Algorithm, Kakutani'sProblem, Syracuse Algorithm, Syracuse Problem, Thwaites Conjecture, and Ulam's Problem(Lagarias 1985). Thwaites (1996) has offered a  1000 reward for resolving the Conjecture. Let 1000 reward for resolving the Conjecture. Let 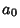 be anInteger. Then the Collatz problem asks if iterating be anInteger. Then the Collatz problem asks if iterating
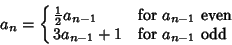 | (1) |
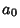 . This question has been tested and found to be true for all numbers . This question has been tested and found to be true for all numbers  (Leavens and Vermeulen 1992), and more recently, (Leavens and Vermeulen 1992), and more recently, 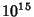 (Vardi 1991, p. 129). The members of theSequence produced by the Collatz are sometimes known as Hailstone Numbers. Because ofthe difficulty in solving this problem, Erdös commented that ``mathematics is not yet ready for such problems''(Lagarias 1985). If Negative numbers are included, there are four known cycles (excluding the trivial 0 cycle): (4, 2, 1),( (Vardi 1991, p. 129). The members of theSequence produced by the Collatz are sometimes known as Hailstone Numbers. Because ofthe difficulty in solving this problem, Erdös commented that ``mathematics is not yet ready for such problems''(Lagarias 1985). If Negative numbers are included, there are four known cycles (excluding the trivial 0 cycle): (4, 2, 1),( , , 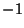 ), ( ), (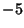 , , 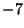 , , 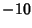 ), and ( ), and ( , , 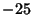 , ,  , , 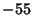 , , 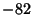 , ,  , , 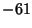 , ,  , ,  , ,  , ,  ). The number of tripling steps needed to reach 1 for ). The number of tripling steps needed to reach 1 for  , 2, ... are 0, 0, 2, 0, 1, 2, 5, 0, 6, ...(Sloane's A006667). , 2, ... are 0, 0, 2, 0, 1, 2, 5, 0, 6, ...(Sloane's A006667).
The Collatz problem was modified by Terras (1976, 1979), who asked if iterating
 | (2) |
 . If Negative numbers are included, there are 4 known cycles: (1, 2),( . If Negative numbers are included, there are 4 known cycles: (1, 2),(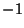 ), ( ), (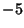 , , 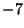 , , 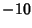 ), and ( ), and ( , , 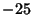 , ,  , , 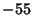 , , 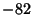 , ,  , , 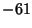 , ,  , ,  , ,  , ,  ). It is aspecial case of the ``generalized Collatz problem'' with ). It is aspecial case of the ``generalized Collatz problem'' with  , , 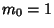 , ,  , , 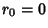 , and , and  . Terras (1976, 1979)also proved that the set of Integers . Terras (1976, 1979)also proved that the set of Integers   has stopping time has stopping time 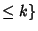 has a limitingasymptotic density has a limitingasymptotic density  , such that if , such that if 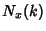 is the number of is the number of  such that such that  and and  , thenthe limit , thenthe limit
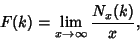 | (3) |
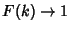 as as  , so almost all Integers have a finite stopping time. Finally, for all , so almost all Integers have a finite stopping time. Finally, for all 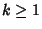 , ,
 | (4) |
(Lagarias 1985).
Conway proved that the original Collatz problem has no nontrivial cycles of length  . Lagarias (1985) showed thatthere are no nontrivial cycles with length . Lagarias (1985) showed thatthere are no nontrivial cycles with length  . Conway (1972) also proved that Collatz-type problems can beformally Undecidable. . Conway (1972) also proved that Collatz-type problems can beformally Undecidable.
A generalization of the Collatz Problem lets  be a Positive Integer and be a Positive Integer and  , ..., , ..., 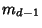 be Nonzero Integers. Also let be Nonzero Integers. Also let 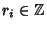 satisfy satisfy
 | (8) |
 | (9) |
 defines a generalized Collatz mapping. An equivalent form is defines a generalized Collatz mapping. An equivalent form is
 | (10) |
 where where  , ..., , ...,  are Integers and are Integers and 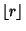 is the FloorFunction. The problem is connected with Ergodic Theory and Markov Chains (Matthews 1995). Matthews (1995) obtained the following table for the mapping is the FloorFunction. The problem is connected with Ergodic Theory and Markov Chains (Matthews 1995). Matthews (1995) obtained the following table for the mapping
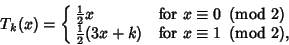 | (11) |
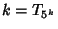 . .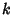 | # Cycles | Max. Cycle Length | | 0 | 5 | 27 | | 1 | 10 | 34 | | 2 | 13 | 118 | | 3 | 17 | 118 | | 4 | 19 | 118 | | 5 | 21 | 165 | | 6 | 23 | 433 |
Matthews and Watts (1984) proposed the following conjectures. - 1. If
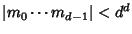 , then all trajectories , then all trajectories  for for  eventually cycle. eventually cycle. - 2. If
 , then almost all trajectories , then almost all trajectories  for for  are divergent,except for an exceptional set of Integers are divergent,except for an exceptional set of Integers  satisfying satisfying
- 3. The number of cycles is finite.
- 4. If the trajectory
 for for  is not eventually cyclic, then the iterates are uniformlydistribution mod is not eventually cyclic, then the iterates are uniformlydistribution mod  for each for each  , with , with | |  | (12) |
for  . .
Matthews believes that the map
 | (13) |
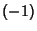 or or  , and offers a $100 (Australian?) prizefor a proof.See also Hailstone Number , and offers a $100 (Australian?) prizefor a proof.See also Hailstone Number
References
Applegate, D. and Lagarias, J. C. ``Density Bounds for the  Problem 1. Tree-Search Method.'' Math. Comput. 64, 411-426, 1995. Problem 1. Tree-Search Method.'' Math. Comput. 64, 411-426, 1995.Applegate, D. and Lagarias, J. C. ``Density Bounds for the  Problem 2. Krasikov Inequalities.'' Math. Comput. 64, 427-438, 1995. Problem 2. Krasikov Inequalities.'' Math. Comput. 64, 427-438, 1995. Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972. Burckel, S. ``Functional Equations Associated with Congruential Functions.'' Theor. Comp. Sci. 123, 397-406, 1994. Conway, J. H. ``Unpredictable Iterations.'' Proc. 1972 Number Th. Conf., University of Colorado, Boulder, Colorado, pp. 49-52, 1972. Crandall, R. ``On the ` ' Problem.'' Math. Comput. 32, 1281-1292, 1978. ' Problem.'' Math. Comput. 32, 1281-1292, 1978. Everett, C. ``Iteration of the Number Theoretic Function  , ,  .'' Adv. Math. 25, 42-45, 1977. .'' Adv. Math. 25, 42-45, 1977. Guy, R. K. ``Collatz's Sequence.'' §E16 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 215-218, 1994. Lagarias, J. C. ``The  Problem and Its Generalizations.'' Amer. Math. Monthly 92, 3-23, 1985. http://www.cecm.sfu.ca/organics/papers/lagarias/. Problem and Its Generalizations.'' Amer. Math. Monthly 92, 3-23, 1985. http://www.cecm.sfu.ca/organics/papers/lagarias/. Leavens, G. T. and Vermeulen, M. `` Search Programs.'' Comput. Math. Appl. 24, 79-99, 1992. Search Programs.'' Comput. Math. Appl. 24, 79-99, 1992. Matthews, K. R. ``The Generalized  Mapping.'' http://www.maths.uq.oz.au/~krm/survey.ps. Rev. Mar. 30, 1999. Mapping.'' http://www.maths.uq.oz.au/~krm/survey.ps. Rev. Mar. 30, 1999. Matthews, K. R. ``A Generalized  Conjecture.'' [$100 Reward for a Proof.] ftp://www.maths.uq.edu.au/pub/krm/gnubc/challenge. Conjecture.'' [$100 Reward for a Proof.] ftp://www.maths.uq.edu.au/pub/krm/gnubc/challenge. Matthews, K. R. and Watts, A. M. ``A Generalization of Hasses's Generalization of the Syracuse Algorithm.'' Acta Arith. 43, 167-175, 1984. Sloane, N. J. A. SequenceA006667/M0019in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Terras, R. ``A Stopping Time Problem on the Positive Integers.'' Acta Arith. 30, 241-252, 1976. Terras, R. ``On the Existence of a Density.'' Acta Arith. 35, 101-102, 1979. Thwaites, B. ``Two Conjectures, or How to win  1100.'' Math.Gaz. 80, 35-36, 1996. 1100.'' Math.Gaz. 80, 35-36, 1996. Vardi, I. ``The  Problem.'' Ch. 7 in Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 129-137, 1991. Problem.'' Ch. 7 in Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 129-137, 1991.
|
![]() 1000 reward for resolving the Conjecture. Let
1000 reward for resolving the Conjecture. Let ![]() be anInteger. Then the Collatz problem asks if iterating
be anInteger. Then the Collatz problem asks if iterating![]() . Lagarias (1985) showed thatthere are no nontrivial cycles with length
. Lagarias (1985) showed thatthere are no nontrivial cycles with length ![]() . Conway (1972) also proved that Collatz-type problems can beformally Undecidable.
. Conway (1972) also proved that Collatz-type problems can beformally Undecidable.![]() be a Positive Integer and
be a Positive Integer and ![]() , ...,
, ..., ![]() be Nonzero Integers. Also let
be Nonzero Integers. Also let ![]() satisfy
satisfy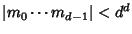 , then all trajectories
, then all trajectories  for
for  eventually cycle.
eventually cycle. , then almost all trajectories
, then almost all trajectories  for
for  are divergent,except for an exceptional set of Integers
are divergent,except for an exceptional set of Integers  satisfying
satisfying
 for
for  is not eventually cyclic, then the iterates are uniformlydistribution mod
is not eventually cyclic, then the iterates are uniformlydistribution mod  for each
for each  , with
, with

 .
.
![]() Problem 1. Tree-Search Method.'' Math. Comput. 64, 411-426, 1995.
Problem 1. Tree-Search Method.'' Math. Comput. 64, 411-426, 1995.![]() Problem 2. Krasikov Inequalities.'' Math. Comput. 64, 427-438, 1995.
Problem 2. Krasikov Inequalities.'' Math. Comput. 64, 427-438, 1995.![]() ' Problem.'' Math. Comput. 32, 1281-1292, 1978.
' Problem.'' Math. Comput. 32, 1281-1292, 1978.![]() ,
, ![]() .'' Adv. Math. 25, 42-45, 1977.
.'' Adv. Math. 25, 42-45, 1977.![]() Problem and Its Generalizations.'' Amer. Math. Monthly 92, 3-23, 1985. http://www.cecm.sfu.ca/organics/papers/lagarias/.
Problem and Its Generalizations.'' Amer. Math. Monthly 92, 3-23, 1985. http://www.cecm.sfu.ca/organics/papers/lagarias/.![]() Search Programs.'' Comput. Math. Appl. 24, 79-99, 1992.
Search Programs.'' Comput. Math. Appl. 24, 79-99, 1992.![]() Mapping.'' http://www.maths.uq.oz.au/~krm/survey.ps. Rev. Mar. 30, 1999.
Mapping.'' http://www.maths.uq.oz.au/~krm/survey.ps. Rev. Mar. 30, 1999.![]() Conjecture.'' [$100 Reward for a Proof.] ftp://www.maths.uq.edu.au/pub/krm/gnubc/challenge.
Conjecture.'' [$100 Reward for a Proof.] ftp://www.maths.uq.edu.au/pub/krm/gnubc/challenge.![]() 1100.'' Math.Gaz. 80, 35-36, 1996.
1100.'' Math.Gaz. 80, 35-36, 1996.![]() Problem.'' Ch. 7 in Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 129-137, 1991.
Problem.'' Ch. 7 in Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 129-137, 1991.