Subspace
Let 
be a Real Vector Space (e.g., the real continuous functions 
on aClosed Interval 
, 2-D Euclidean Space 
, the twice differentiable real functions 
on, etc.). Then 
is a real Subspace of if is a Subset of and, for every
, 
and 
(the Reals), 
and 
. Let 
be a homogeneous system of linear equations in 
, ..., 
. Then theSubset 
of 
which consists of all solutions of the system is a subspace of .
More generally, let 
be a Field with 
, where 
is Prime, and let 
denote the 
-DVector Space over . The number of 
-D linear subspaces of is
where this is the q-Binomial Coefficient (Aigner 1979, Exton 1983). The asymptotic limit is
where
 |  |  | |
 | |  |
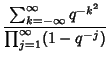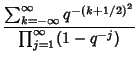(Finch). The case
gives the q-Analog of the Wallis Formula.See also q-Binomial Coefficient, Subfield, Submanifold
References
Aigner, M. Combinatorial Theory. New York: Springer-Verlag, 1979. Exton, H. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/dig/dig.html
-Hypergeometric Functions and Applications. New York: Halstead Press, 1983.
- Kissing Number
- Kiss Surface
- Kite
- Klarner-Rado Sequence
- Klarner's Theorem
- Klein-Beltrami Model
- Klein Bottle
- Klein Four-Group
- Klein-Gordon Equation
- Kleinian Group
- Klein Quartic
- Klein's Absolute Invariant
- Klein's Equation
- Klein's Theorem
- Kloosterman's Sum
- k-Matrix
- Knapsack Problem
- Kneser-Sommerfeld Formula
- Knights of the Round Table
- Knights Problem
- Knight's Tour
- Knot
- Knot Complement
- Knot Curve
- Knot Determinant