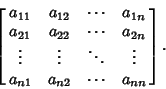| 释义 |
Symmetric MatrixA symmetric matrix is a Square Matrix which satisfies  where where 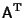 denotes theTranspose, so denotes theTranspose, so  . This also implies . This also implies
 | (1) |
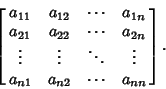 | (2) |
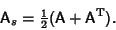 | (3) |
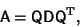 | (4) |
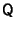 is an Orthogonal Matrix and is an Orthogonal Matrix and 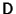 is a Diagonal Matrix. This is equivalent to theMatrix equation is a Diagonal Matrix. This is equivalent to theMatrix equation
 | (5) |
 | (6) |
 , where , where  . Therefore, the diagonal elements of . Therefore, the diagonal elements of 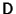 are the Eigenvalues of are the Eigenvalues of  , and the columns of , and the columns of 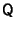 are the corresponding Eigenvectors.See also Antisymmetric Matrix, Skew Symmetric Matrix are the corresponding Eigenvectors.See also Antisymmetric Matrix, Skew Symmetric Matrix
References
Nash, J. C. ``Real Symmetric Matrices.'' Ch. 10 in Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation, 2nd ed. Bristol, England: Adam Hilger, pp. 119-134, 1990.
|
![]() where
where ![]() denotes theTranspose, so
denotes theTranspose, so ![]() . This also implies
. This also implies