| 释义 |
Triangular NumberA Figurate Number of the form 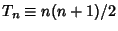 obtained by building up regular triangles out of dots. The firstfew triangle numbers are 1, 3, 6, 10, 15, 21, ... (Sloane's A000217). obtained by building up regular triangles out of dots. The firstfew triangle numbers are 1, 3, 6, 10, 15, 21, ... (Sloane's A000217).  gives the number and arrangement ofBowling pins, while gives the number and arrangement ofBowling pins, while 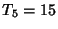 gives the number and arrangement of balls in Billiards. Triangular numberssatisfy the Recurrence Relation gives the number and arrangement of balls in Billiards. Triangular numberssatisfy the Recurrence Relation
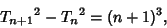 | (1) |
and
 | (5) |
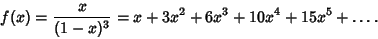 | (6) |
Every triangular number is also a Hexagonal Number, since
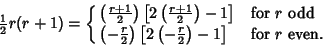 | (7) |
Interesting identities involving triangular numbers and Square Numbers are
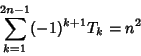 | (9) |
 | (10) |
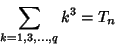 | (11) |
 Odd and Odd and
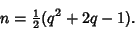 | (12) |
All Even Perfect Numbers are triangular  with Prime with Prime 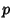 . Furthermore, every EvenPerfect Number . Furthermore, every EvenPerfect Number  is of the form is of the form
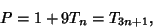 | (13) |
 is a triangular number with is a triangular number with 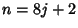 (Eaton 1995, 1996). Therefore, the nested expression (Eaton 1995, 1996). Therefore, the nested expression
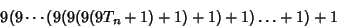 | (14) |
 . An Integer . An Integer  is a triangular numberIff is a triangular numberIff 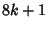 is a Square Number is a Square Number 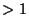 . .
The numbers 1, 36, 1225, 41616, 1413721, 48024900, ... (Sloane's A001110) are Square Triangular Numbers, i.e., numbers which are simultaneously triangular and Square (Pietenpol1962). Numbers which are simultaneously triangular and Tetrahedral satisfy theBinomial Coefficient equation
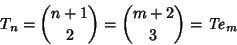 | (15) |
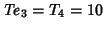 , , 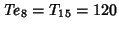 , ,  , and , and 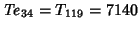 (Guy 1994, p. 147). (Guy 1994, p. 147).
The smallest of two Integers forwhich  is four times a triangular number is 5 (Cesaro 1886; Le Lionnais 1983, p. 56). The only FibonacciNumbers which are triangular are 1, 3, 21, and 55 (Ming 1989), and the only Pell Number which istriangular is 1 (McDaniel 1996). The Beast Number 666 is triangular, since is four times a triangular number is 5 (Cesaro 1886; Le Lionnais 1983, p. 56). The only FibonacciNumbers which are triangular are 1, 3, 21, and 55 (Ming 1989), and the only Pell Number which istriangular is 1 (McDaniel 1996). The Beast Number 666 is triangular, since
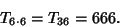 | (16) |
Fermat's Polygonal Number Theorem states that every Positive Integer is a sum of most threeTriangular Numbers, four Square Numbers, five PentagonalNumbers, and  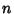 -Gauß -Gauß  proved thetriangular case, and noted the event in his diary on July 10, 1796, with the notation proved thetriangular case, and noted the event in his diary on July 10, 1796, with the notation
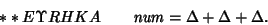 | (17) |
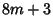 is a sum of three OddDirichlet is a sum of three OddDirichlet  derived the number of ways in which an Integer derived the number of ways in which an Integer 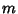 can be expressed as the sum of three triangular numbers (Duke 1997). The result is particularly simple for a Prime ofthe form can be expressed as the sum of three triangular numbers (Duke 1997). The result is particularly simple for a Prime ofthe form 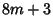 , in which case it is the number of squares mod , in which case it is the number of squares mod 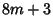 minus the number of nonsquares mod minus the number of nonsquares mod 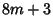 in theInterval in theInterval 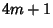 (Deligne 1973). (Deligne 1973).
The only triangular numbers which are the Product of three consecutive Integers are6, 120, 210, 990, 185136, 258474216 (Guy 1994, p. 148). See also Figurate Number, Pronic Number, Square Triangular Number
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.Bellew, D. W. and Weger, R. C. ``Repdigit Triangular Numbers.'' J. Recr. Math. 8, 96-97, 1975-76. Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 33-38, 1996. Deligne, P. ``La Conjecture de Weil.'' Inst. Hautes Études Sci. Pub. Math. 43, 273-308, 1973. Dudeney, H. E. Amusements in Mathematics. New York: Dover, pp. 67 and 167, 1970. Duke, W. ``Some Old Problems and New Results about Quadratic Forms.'' Not. Amer. Math. Soc. 44, 190-196, 1997. Eaton, C. F. ``Problem 1482.'' Math. Mag. 68, 307, 1995. Eaton, C. F. ``Perfect Number in Terms of Triangular Numbers.'' Solution to Problem 1482. Math. Mag. 69, 308-309, 1996. Guy, R. K. ``Sums of Squares'' and ``Figurate Numbers.'' §C20 and §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138 and 147-150, 1994. Hindin, H. ``Stars, Hexes, Triangular Numbers and Pythagorean Triples.'' J. Recr. Math. 16, 191-193, 1983-1984. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 56, 1983. McDaniel, W. L. ``Triangular Numbers in the Pell Sequence.'' Fib. Quart. 34, 105-107, 1996. Ming, L. ``On Triangular Fibonacci Numbers.'' Fib. Quart. 27, 98-108, 1989. Pappas, T. ``Triangular, Square & Pentagonal Numbers.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989. Pietenpol, J. L ``Square Triangular Numbers.'' Amer. Math. Monthly 169, 168-169, 1962. Satyanarayana, U. V. ``On the Representation of Numbers as the Sum of Triangular Numbers.'' Math. Gaz. 45, 40-43, 1961. Sloane, N. J. A. SequencesA000217/M2535and A001110/M5259in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
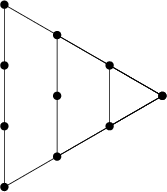
![]() obtained by building up regular triangles out of dots. The firstfew triangle numbers are 1, 3, 6, 10, 15, 21, ... (Sloane's A000217).
obtained by building up regular triangles out of dots. The firstfew triangle numbers are 1, 3, 6, 10, 15, 21, ... (Sloane's A000217). ![]() gives the number and arrangement ofBowling pins, while
gives the number and arrangement ofBowling pins, while ![]() gives the number and arrangement of balls in Billiards. Triangular numberssatisfy the Recurrence Relation
gives the number and arrangement of balls in Billiards. Triangular numberssatisfy the Recurrence Relation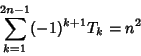

![]() with Prime
with Prime ![]() . Furthermore, every EvenPerfect Number
. Furthermore, every EvenPerfect Number ![]() is of the form
is of the form![]() is four times a triangular number is 5 (Cesaro 1886; Le Lionnais 1983, p. 56). The only FibonacciNumbers which are triangular are 1, 3, 21, and 55 (Ming 1989), and the only Pell Number which istriangular is 1 (McDaniel 1996). The Beast Number 666 is triangular, since
is four times a triangular number is 5 (Cesaro 1886; Le Lionnais 1983, p. 56). The only FibonacciNumbers which are triangular are 1, 3, 21, and 55 (Ming 1989), and the only Pell Number which istriangular is 1 (McDaniel 1996). The Beast Number 666 is triangular, since![]()
![]() -Gauß
-Gauß ![]() proved thetriangular case, and noted the event in his diary on July 10, 1796, with the notation
proved thetriangular case, and noted the event in his diary on July 10, 1796, with the notation