Tangent
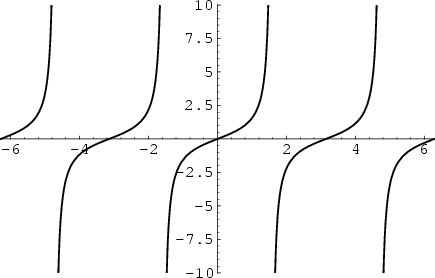
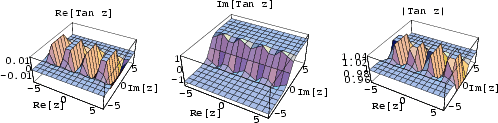
The tangent function is defined by
 | (1) |
is the Sine function and 
is the Cosine function. The word ``tangent,'' however, alsohas an important related meaning as a Line or Plane which touches a given curve or solid at a single point. These geometrical objects are then called a Tangent Line or Tangent Plane, respectively.The Maclaurin Series for the tangent function is
 |  |  | |
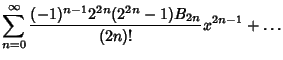|  | (2) |
where
is a Bernoulli Number.
is Irrational for any Rational 
, which can be proved by writing as a Continued Fraction
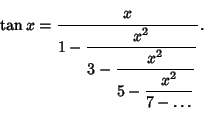 | (3) |
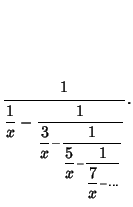| |  | (4) |
An interesting identity involving the Product of tangents is
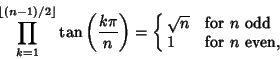 | (5) |
is the Floor Function. Another tangent identity is | (6) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Circular Functions.'' §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972. Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972. Spanier, J. and Oldham, K. B. ``The Tangent 
and Cotangent 
Functions.'' Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.
- Rodrigues Formula
- Rodrigues's Curvature Formula
- Rogers-Ramanujan Continued Fraction
- Rogers-Ramanujan Identities
- Rolle's Theorem
- Roman Coefficient
- Roman Factorial
- Roman Numeral
- Roman Surface
- Roman Symbol
- Romberg Integration
- Rook Number
- Rook Reciprocity Theorem
- Rooks Problem
- Room Square
- Root
- Root Dragging Theorem
- Rooted Tree
- Root Linear Coefficient Theorem
- Root-Mean-Square
- Root of Unity
- Root (Radical)
- Root Test
- Root (Tree)
- Rosatti's Theorem