| 释义 |
Tau FunctionA function 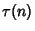 related to the Divisor Function related to the Divisor Function 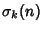 , also sometimes called Ramanujan's TauFunction. It is given by the Generating Function , also sometimes called Ramanujan's TauFunction. It is given by the Generating Function
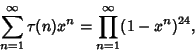 | (1) |
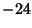 , 252, , 252, 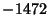 , 4380, ... (Sloane's A000594). , 4380, ... (Sloane's A000594). 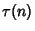 is also given by is also given by
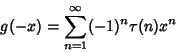 | (2) |
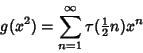 | (3) |
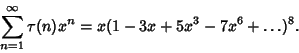 | (4) |
In Ore's Conjecture, the tau function appears as the number of Divisors of 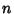 .Ramanujan .Ramanujan  conjectured and Mordell proved that if conjectured and Mordell proved that if 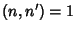 , then , then
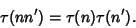 | (5) |
 conjectured and Watson proved that conjectured and Watson proved that 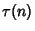 is divisible by 691 for almost all is divisible by 691 for almost all 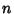 . If . If
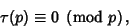 | (6) |
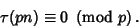 | (7) |
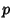 for which the first equation holds are for which the first equation holds are 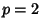 , 3, 5, 7, 23. , 3, 5, 7, 23.
Ramanujan  also studied also studied
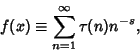 | (8) |
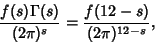 | (9) |
 Tau-Dirichlet Series conjecture alleges that all nontrivial zeros of Tau-Dirichlet Series conjecture alleges that all nontrivial zeros of  lie on the line lie on the line 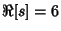 . .  can be split up into can be split up into
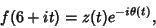 | (10) |
The Summatory tau function is given by
 | (13) |
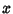 is an Integer, the last term is an Integer, the last term 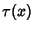 should be replaced by should be replaced by  . .
Ramanujan's tau theta function 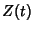 is a Real function for Real is a Real function for Real 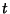 and isanalogous to the Riemann-Siegel Function and isanalogous to the Riemann-Siegel Function  . The number of zeros in the critical stripfrom . The number of zeros in the critical stripfrom 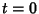 to to 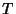 is given by is given by
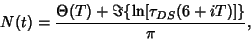 | (14) |
 is the Riemann Theta Function and is the Riemann Theta Function and 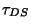 is the Tau-Dirichlet Series, defined by is the Tau-Dirichlet Series, defined by
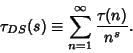 | (15) |
 conjectured that the nontrivial zeros of the function are all real. conjectured that the nontrivial zeros of the function are all real.
Ramanujan's 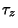 function is defined by function is defined by
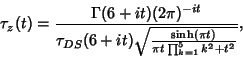 | (16) |
 is the Tau-Dirichlet Series.See also Ore's Conjecture, Tau Conjecture, Tau-Dirichlet Series is the Tau-Dirichlet Series.See also Ore's Conjecture, Tau Conjecture, Tau-Dirichlet Series
References
Hardy, G. H. ``Ramanujan's Function 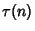 .'' Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959. .'' Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.Sloane, N. J. A. SequenceA000594/M5153in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
![]() related to the Divisor Function
related to the Divisor Function ![]() , also sometimes called Ramanujan's TauFunction. It is given by the Generating Function
, also sometimes called Ramanujan's TauFunction. It is given by the Generating Function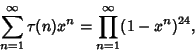
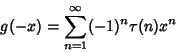
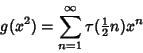
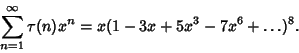
![]() .Ramanujan
.Ramanujan ![]() conjectured and Mordell proved that if
conjectured and Mordell proved that if ![]() , then
, then![]() also studied
also studied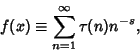
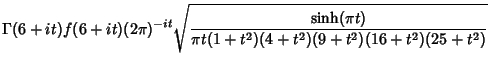
![]() is a Real function for Real
is a Real function for Real ![]() and isanalogous to the Riemann-Siegel Function
and isanalogous to the Riemann-Siegel Function ![]() . The number of zeros in the critical stripfrom
. The number of zeros in the critical stripfrom ![]() to
to ![]() is given by
is given by
![]() function is defined by
function is defined by
![]() .'' Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.
.'' Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.