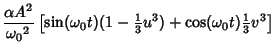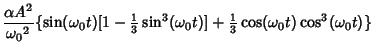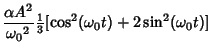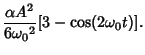“Simple Harmonic Motion Quadratic Perturbation”的概念、定义、习题解题方法及翻译-数学辞典

单词

Simple Harmonic Motion Quadratic Perturbation

释义

Simple Harmonic Motion Quadratic Perturbation

Given a simple harmonic oscillator with a quadratic perturbation ,

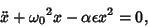(1)

find the first-order solution using a perturbation method. Write

(2)

(3)

Plugging (2) and (3) back into (1) gives

(4)

Keeping only terms of order

and lower and grouping, we obtain

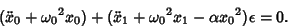(5)

Since this equation must hold for all Powers of

, we can separate it into the two differential equations

(6)

(7)

The solution to (6) is just

(8)

Setting our clock so that

gives

(9)

Plugging this into (7) then gives

(10)

The two homogeneous solutions to (10) are

			(11)
			(12)

The particular solution to (10) is therefore given by

(13)

where

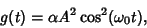(14)

and the Wronskian is

Plugging everything into (13),

Now let

Then

Plugging

and (21) into (2), we obtain the solution

(22)

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。