| 释义 |
TensorAn 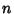 th-Rank tensor of order th-Rank tensor of order 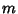 is a mathematical object in is a mathematical object in 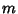 -dimensional space which has -dimensional space which has 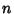 indices and indices and  components and obeys certain transformation rules. Each index of a tensor ranges over the number ofdimensions of Space. If the components of any tensor of any Rank vanish in one particularcoordinate system, they vanish in all coordinate systems. components and obeys certain transformation rules. Each index of a tensor ranges over the number ofdimensions of Space. If the components of any tensor of any Rank vanish in one particularcoordinate system, they vanish in all coordinate systems.
Zeroth-Rank tensors are called Scalars, and first-Ranktensors are called Vectors. In tensor notation, a vector v would be written 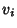 , where , where 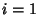 ,..., ,..., 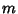 . Tensor notation can provide a very concise way of writing vector and more general identities. For example, intensor notation, the Dot Product . Tensor notation can provide a very concise way of writing vector and more general identities. For example, intensor notation, the Dot Product 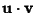 is simply written is simply written
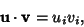 | (1) |
 stands for stands for 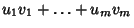 . Similarly, the Cross Product can be concisely written as . Similarly, the Cross Product can be concisely written as
 | (2) |
 is the Levi-Civita Tensor. is the Levi-Civita Tensor.
Second-Rank tensors resemble square Matrices.Contravariant second-Rank tensors are objects which transform as
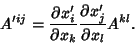 | (3) |
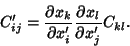 | (4) |
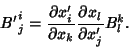 | (5) |
If two tensors  and and  have the same Rank and the same Covariantand Contravariant indices, then have the same Rank and the same Covariantand Contravariant indices, then
 | (6) |
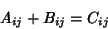 | (7) |
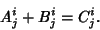 | (8) |
A transformation of the variables of a tensor changes the tensor into another whose components are linear HomogeneousFunctions of the components of the original tensor. See also Antisymmetric Tensor, Curl, Divergence, Gradient, Irreducible Tensor,Isotropic Tensor, Jacobi Tensor, Ricci Tensor, Riemann Tensor, Scalar, SymmetricTensor, Torsion Tensor, Vector, Weyl Tensor
References
 Tensors TensorsAbraham, R.; Marsden, J. E.; and Ratiu, T. S. Manifolds, Tensor Analysis, and Applications. New York: Springer-Verlag, 1991. Akivis, M. A. and Goldberg, V. V. An Introduction to Linear Algebra and Tensors. New York: Dover, 1972. Arfken, G. ``Tensor Analysis.'' Ch. 3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 118-167, 1985. Aris, R. Vectors, Tensors, and the Basic Equations of Fluid Mechanics. New York: Dover, 1989. Bishop, R. and Goldberg, S. Tensor Analysis on Manifolds. New York: Dover, 1980. Jeffreys, H. Cartesian Tensors. Cambridge, England: Cambridge University Press, 1931. Joshi, A. W. Matrices and Tensors in Physics, 3rd ed. New York: Wiley, 1995. Lass, H. Vector and Tensor Analysis. New York: McGraw-Hill, 1950. Lawden, D. F. An Introduction to Tensor Calculus, Relativity, and Cosmology, 3rd ed. Chichester, England: Wiley, 1982. McConnell, A. J. Applications of Tensor Analysis. New York: Dover, 1947. Morse, P. M. and Feshbach, H. ``Vector and Tensor Formalism.'' §1.5 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 44-54, 1953. Simmonds, J. G. A Brief on Tensor Analysis, 2nd ed. New York: Springer-Verlag, 1994. Sokolnikoff, I. S. Tensor Analysis--Theory and Applications, 2nd ed. New York: Wiley, 1964. Synge, J. L. and Schild, A. Tensor Calculus. New York: Dover, 1978. Wrede, R. C. Introduction to Vector and Tensor Analysis. New York: Wiley, 1963.
|
![]() th-Rank tensor of order
th-Rank tensor of order ![]() is a mathematical object in
is a mathematical object in ![]() -dimensional space which has
-dimensional space which has ![]() indices and
indices and ![]() components and obeys certain transformation rules. Each index of a tensor ranges over the number ofdimensions of Space. If the components of any tensor of any Rank vanish in one particularcoordinate system, they vanish in all coordinate systems.
components and obeys certain transformation rules. Each index of a tensor ranges over the number ofdimensions of Space. If the components of any tensor of any Rank vanish in one particularcoordinate system, they vanish in all coordinate systems.![]() , where
, where ![]() ,...,
,..., ![]() . Tensor notation can provide a very concise way of writing vector and more general identities. For example, intensor notation, the Dot Product
. Tensor notation can provide a very concise way of writing vector and more general identities. For example, intensor notation, the Dot Product ![]() is simply written
is simply written ![]() and
and ![]() have the same Rank and the same Covariantand Contravariant indices, then
have the same Rank and the same Covariantand Contravariant indices, then![]() Tensors
Tensors