| 释义 |
Kolmogorov-Arnold-Moser TheoremA theorem outlined in 1954 by Kolmogorov which was subsequently proved in the 1960s by Arnold and Moser (Tabor 1989,p. 105). It gives conditions under which Chaos is restricted in extent. Moser's 1962 proof was valid forTwist Maps
In 1963, Arnold produced a proof for Hamiltonian systems
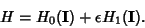 | (3) |
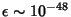 , although this has since been significantly increased. Arnold's proof required , although this has since been significantly increased. Arnold's proof required  , and Moser's original proof required , and Moser's original proof required 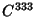 . Subsequently, Moser's version has beenreduced to . Subsequently, Moser's version has beenreduced to 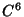 , then , then 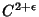 , although counterexamples are known for , although counterexamples are known for  . Conditions for applicability of the KAMtheorem are: . Conditions for applicability of the KAMtheorem are:- 1. small perturbations,
- 2. smooth perturbations, and
- 3. sufficiently irrational Winding Number.
Moser considered an integrable Hamiltonian function 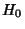 with a Torus with a Torus 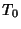 and set of frequencies and set of frequencies 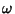 having anincommensurate frequency vector having anincommensurate frequency vector 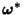 (i.e., (i.e., 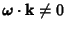 for all Integers for all Integers 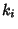 ). Let ). Let 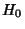 be perturbed by some periodic function be perturbed by some periodic function 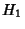 . The KAM theorem states that, if . The KAM theorem states that, if 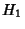 is small enough, then foralmost every is small enough, then foralmost every 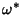 there exists an invariant Torus there exists an invariant Torus 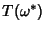 of the perturbed system such that of the perturbed system such that 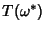 is ``close to'' is ``close to'' 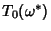 . Moreover, the Tori . Moreover, the Tori 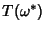 form a set of Positive measures whosecomplement has a measure which tends to zero as form a set of Positive measures whosecomplement has a measure which tends to zero as 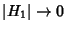 . A useful paraphrase of the KAM theorem is, ``For sufficientlysmall perturbation, almost all Tori (excluding those with rational frequency vectors) are preserved.'' Thetheorem thus explicitly excludes Tori with rationally related frequencies, that is, . A useful paraphrase of the KAM theorem is, ``For sufficientlysmall perturbation, almost all Tori (excluding those with rational frequency vectors) are preserved.'' Thetheorem thus explicitly excludes Tori with rationally related frequencies, that is, 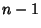 conditions of theform conditions of theform
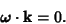 | (4) |
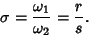 | (5) |
 is Irrational. KAM shows that the preserved Tori satisfy the irrationality condition is Irrational. KAM shows that the preserved Tori satisfy the irrationality condition
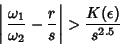 | (6) |
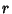 and and 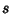 , although not much is known about , although not much is known about 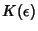 . .
The KAM theorem broke the deadlock of the small divisor problem in classical perturbation theory, and provides the startingpoint for an understanding of the appearance of Chaos. For a Hamiltonian System, the IsoenergeticNondegeneracy condition
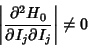 | (7) |
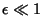 . The Arnold versionstates that . The Arnold versionstates that
 | (8) |
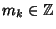 . This condition is less restrictive than Moser's, so fewer points are excluded.See also Chaos, Hamiltonian System, Quasiperiodic Function, Torus . This condition is less restrictive than Moser's, so fewer points are excluded.See also Chaos, Hamiltonian System, Quasiperiodic Function, Torus
References
Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.
|
![]() with a Torus
with a Torus ![]() and set of frequencies
and set of frequencies ![]() having anincommensurate frequency vector
having anincommensurate frequency vector ![]() (i.e.,
(i.e., ![]() for all Integers
for all Integers ![]() ). Let
). Let ![]() be perturbed by some periodic function
be perturbed by some periodic function ![]() . The KAM theorem states that, if
. The KAM theorem states that, if ![]() is small enough, then foralmost every
is small enough, then foralmost every ![]() there exists an invariant Torus
there exists an invariant Torus ![]() of the perturbed system such that
of the perturbed system such that ![]() is ``close to''
is ``close to'' ![]() . Moreover, the Tori
. Moreover, the Tori ![]() form a set of Positive measures whosecomplement has a measure which tends to zero as
form a set of Positive measures whosecomplement has a measure which tends to zero as ![]() . A useful paraphrase of the KAM theorem is, ``For sufficientlysmall perturbation, almost all Tori (excluding those with rational frequency vectors) are preserved.'' Thetheorem thus explicitly excludes Tori with rationally related frequencies, that is,
. A useful paraphrase of the KAM theorem is, ``For sufficientlysmall perturbation, almost all Tori (excluding those with rational frequency vectors) are preserved.'' Thetheorem thus explicitly excludes Tori with rationally related frequencies, that is, ![]() conditions of theform
conditions of theform