| 释义 |
Abel's IdentityGiven a homogeneous linear Second-Order Ordinary Differential Equation,
 | (1) |
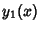 and and  . Then . Then
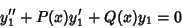 | (2) |
 | (3) |
 (3) minus (3) minus  (2), (2),
 | (4) |
 | (5) |
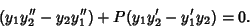 | (6) |
Plugging 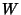 and and  into (6) gives into (6) gives
 | (9) |
 | (10) |
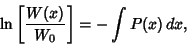 | (11) |
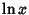 is the Natural Logarithm. Exponentiation then yields Abel's identity is the Natural Logarithm. Exponentiation then yields Abel's identity
 | (12) |
 is a constant of integration.See also Ordinary Differential Equation--Second-Order is a constant of integration.See also Ordinary Differential Equation--Second-Order
References
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, pp. 118, 262, 277, and 355, 1986. |