| 释义 |
ContinuumThe nondenumerable set of Real Numbers, denoted 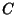 . It satisfies . It satisfies
 | (1) |
 | (2) |
 is Aleph-0. It is also true that is Aleph-0. It is also true that
 | (3) |
 | (4) |
 on a Line (orLine Segment) as in a Plane, a 3-D Space, or finite Hyperspace, since all these Sets can be put into a One-to-One correspondence with each other. on a Line (orLine Segment) as in a Plane, a 3-D Space, or finite Hyperspace, since all these Sets can be put into a One-to-One correspondence with each other.
The Georg Cantor,  holds that theCardinal Number of the continuum is the same as that of Aleph-1. The surprising truth isthat this proposition is Undecidable, since neither it nor its converse contradicts the tenets of SetTheory. holds that theCardinal Number of the continuum is the same as that of Aleph-1. The surprising truth isthat this proposition is Undecidable, since neither it nor its converse contradicts the tenets of SetTheory. See also Aleph-0, Aleph-1, Continuum Hypothesis,Denumerable Set
|
![]() . It satisfies
. It satisfies![]() holds that theCardinal Number of the continuum is the same as that of Aleph-1. The surprising truth isthat this proposition is Undecidable, since neither it nor its converse contradicts the tenets of SetTheory.
holds that theCardinal Number of the continuum is the same as that of Aleph-1. The surprising truth isthat this proposition is Undecidable, since neither it nor its converse contradicts the tenets of SetTheory.