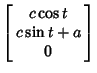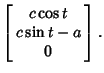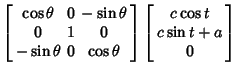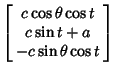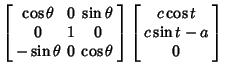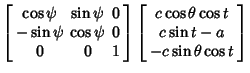| 释义 |
TorusA torus is a surface having Genus 1, and therefore possessing a single ``Hole.'' The usualtorus in 3-D space is shaped like a donut, but the concept of the torus is extremely useful in higher dimensional space aswell. One of the more common uses of 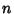 -D tori is in Dynamical Systems. A fundamental resultstates that the Phase Space trajectories of a Hamiltonian System with -D tori is in Dynamical Systems. A fundamental resultstates that the Phase Space trajectories of a Hamiltonian System with  Degrees of Freedom and possessing Degrees of Freedom and possessing 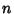 Integrals of Motion lie on an Integrals of Motion lie on an 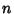 -D Manifold which istopologically equivalent to an -D Manifold which istopologically equivalent to an 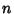 -torus (Tabor 1989). -torus (Tabor 1989).
The usual 3-D ``ring'' torus is known in older literature as an ``Anchor Ring.'' Let the radius from the center ofthe hole to the center of the torus tube be  , and the radius of the tube be , and the radius of the tube be  . Then the equation in CartesianCoordinates is . Then the equation in CartesianCoordinates is
 | (1) |
for  . Three types of torus, known as the Standard Tori, are possible, depending on the relativesizes of . Three types of torus, known as the Standard Tori, are possible, depending on the relativesizes of  and and  . .  corresponds to the Ring Torus (shown above), corresponds to the Ring Torus (shown above),  corresponds to a Horn Toruswhich is tangent to itself at the point (0, 0, 0), and corresponds to a Horn Toruswhich is tangent to itself at the point (0, 0, 0), and 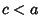 corresponds to a self-intersecting Spindle Torus(Pinkall 1986). corresponds to a self-intersecting Spindle Torus(Pinkall 1986).
If no specification is made, ``torus'' is taken to mean Ring Torus. The three Standard Tori are illustratedbelow, where the first image shows the full torus, the second a cut-away of the bottom half, and the third aCross-Section of a plane passing through the z-Axis. The Standard Tori and their inversions are Cyclides. If the coefficient of  in the formulafor in the formulafor  is changed to is changed to 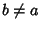 , an Elliptic Torus results. , an Elliptic Torus results.
To compute the metric properties of the ring torus, define the inner and outer radii by
Solving for  and and  gives gives
Then the Surface Area of this torus is
and the Volume can be computed from Pappus's Centroid Theorem
The coefficients of the first and second Fundamental Forms of the torus are given by
giving Riemannian Metric
 | (19) |
 | (20) |
 is a Wedge Product), and Gaussian and MeanCurvatures as is a Wedge Product), and Gaussian and MeanCurvatures as
(Gray 1993, pp. 289-291).
A torus with a Hole in its surface can be turned inside out to yield an identical torus. A torus can beknotted externally or internally, but not both. These two cases are Ambient Isotopies, but notRegular Isotopies. There are therefore three possible ways of embedding a torus with zero or oneKnot.
An arbitrary point 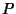 on a torus (not lying in the on a torus (not lying in the  -plane) can havefour Circles drawn through it. The first circle is in the plane of the torus and the second isPerpendicular to it. The third and fourth Circles are called Villarceau Circles(Villarceau 1848, Schmidt 1950, Coxeter 1969, Melnick 1983). -plane) can havefour Circles drawn through it. The first circle is in the plane of the torus and the second isPerpendicular to it. The third and fourth Circles are called Villarceau Circles(Villarceau 1848, Schmidt 1950, Coxeter 1969, Melnick 1983).
To see that two additional Circles exist, consider a coordinate system with originat the center of torus, with  pointing up. Specify the position of pointing up. Specify the position of 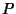 by its Angle by its Angle 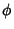 measuredaround the tube of the torus. Define measuredaround the tube of the torus. Define 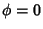 for the circle of points farthest away from the center of the torus (i.e.,the points with for the circle of points farthest away from the center of the torus (i.e.,the points with  ), and draw the x-Axis as the intersection of a plane through the ), and draw the x-Axis as the intersection of a plane through the  -axis andpassing through -axis andpassing through 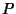 with the with the  -plane. Rotate about the y-Axis by an Angle -plane. Rotate about the y-Axis by an Angle  , where , where
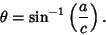 | (23) |
So in 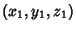 coordinates, equation (1) of the torus becomes coordinates, equation (1) of the torus becomes
 | (26) |
 | (28) |
 | (29) |
 plane, plugging in (23) and factoring gives plane, plugging in (23) and factoring gives
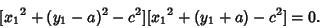 | (30) |
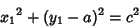 | (31) |
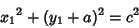 | (32) |
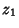 plane. Written in Matrix form with parameter plane. Written in Matrix form with parameter 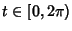 , these are , these are
In the original  coordinates, coordinates,
The point 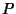 must satisfy must satisfy
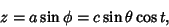 | (37) |
 | (38) |
 and and  gives the Angle gives the Angle 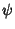 by which the Circle must be rotated about thez-Axis in order to make it pass through by which the Circle must be rotated about thez-Axis in order to make it pass through 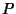 , ,
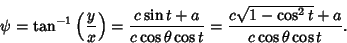 | (39) |
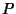 are therefore are therefore
See also Apple, Cyclide, Elliptic Torus, Genus (Surface), Horn Torus, Klein Quartic,Lemon, Ring Torus, Spindle Torus, Spiric Section, Standard Tori, Toroid,Torus Coloring, Torus Cutting
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 131-132, 1987.Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 132-133, 1969. Geometry Center. ``The Torus.'' http://www.geom.umn.edu/zoo/toptype/torus/. Gray, A. ``Tori.'' §11.4 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 218-220 and 289-290, 1993. Melzak, Z. A. Invitation to Geometry. New York: Wiley, pp. 63-72, 1983. Pinkall, U. ``Cyclides of Dupin.'' §3.3 in Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, pp. 28-30, 1986. Schmidt, H. Die Inversion und ihre Anwendungen. Munich: Oldenbourg, p. 82, 1950. Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 71-74, 1989. Villarceau, M. ``Théorème sur le tore.'' Nouv. Ann. Math. 7, 345-347, 1848.
|
![]() -D tori is in Dynamical Systems. A fundamental resultstates that the Phase Space trajectories of a Hamiltonian System with
-D tori is in Dynamical Systems. A fundamental resultstates that the Phase Space trajectories of a Hamiltonian System with ![]() Degrees of Freedom and possessing
Degrees of Freedom and possessing ![]() Integrals of Motion lie on an
Integrals of Motion lie on an ![]() -D Manifold which istopologically equivalent to an
-D Manifold which istopologically equivalent to an ![]() -torus (Tabor 1989).
-torus (Tabor 1989).![]() , and the radius of the tube be
, and the radius of the tube be ![]() . Then the equation in CartesianCoordinates is
. Then the equation in CartesianCoordinates is
![]() in the formulafor
in the formulafor ![]() is changed to
is changed to ![]() , an Elliptic Torus results.
, an Elliptic Torus results.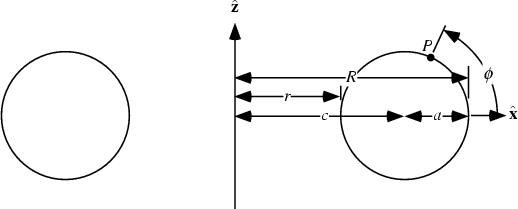

![]() on a torus (not lying in the
on a torus (not lying in the ![]() -plane) can havefour Circles drawn through it. The first circle is in the plane of the torus and the second isPerpendicular to it. The third and fourth Circles are called Villarceau Circles(Villarceau 1848, Schmidt 1950, Coxeter 1969, Melnick 1983).
-plane) can havefour Circles drawn through it. The first circle is in the plane of the torus and the second isPerpendicular to it. The third and fourth Circles are called Villarceau Circles(Villarceau 1848, Schmidt 1950, Coxeter 1969, Melnick 1983). ![]() pointing up. Specify the position of
pointing up. Specify the position of ![]() by its Angle
by its Angle ![]() measuredaround the tube of the torus. Define
measuredaround the tube of the torus. Define ![]() for the circle of points farthest away from the center of the torus (i.e.,the points with
for the circle of points farthest away from the center of the torus (i.e.,the points with ![]() ), and draw the x-Axis as the intersection of a plane through the
), and draw the x-Axis as the intersection of a plane through the ![]() -axis andpassing through
-axis andpassing through ![]() with the
with the ![]() -plane. Rotate about the y-Axis by an Angle
-plane. Rotate about the y-Axis by an Angle ![]() , where
, where