| 释义 |
Ordinary Differential EquationAn ordinary differential equation (frequently abbreviated ODE) is an equality involving a function and itsDerivatives. An ODE of order  is an equation of the form is an equation of the form
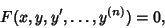 | (1) |
 is a first Derivative with respect to is a first Derivative with respect to 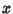 and and  is an is an  th Derivativewith respect to th Derivativewith respect to 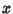 . An ODE of order . An ODE of order  is said to be linear if it is of the form is said to be linear if it is of the form
 | (2) |
 is said to be homogeneous. Confusingly, an ODE of the form is said to be homogeneous. Confusingly, an ODE of the form
 | (3) |
Simple theories exist for first-order (Integrating Factor) and second-order (Sturm-Liouville Theory) ordinarydifferential equations, and arbitrary ODEs with linear constant Coefficients can be solved when theyare of certain factorable forms. Integral transforms such as the Laplace Transform can also be used to solve classesof linear ODEs. Morse and Feshbach (1953, pp. 667-674) give canonical forms and solutions for second-order ODEs.
While there are many general techniques for analytically solving classes of ODEs, the only practical solution technique forcomplicated equations is to use numerical methods (Milne 1970). The most popular of these is the Runge-Kutta Method,but many others have been developed. A vast amount of research and huge numbers of publications have been devoted to thenumerical solution of differential equations, both ordinary and Partial (PDEs) as aresult of their importance in fields as diverse as physics, engineering, economics, and electronics.
The solutions to an ODE satisfy Existence and Uniqueness properties. These can be formallyestablished by Picard's Existence Theorem for certain classes of ODEs. Let a system of first-order ODE be given by
 | (4) |
 , ..., , ...,  and let the functions and let the functions  , where , where  , ..., , ...,  , all be defined in aDomain , all be defined in aDomain  of the of the  -D space of the variables -D space of the variables  , ..., , ..., 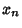 , ,  . Let these functions be continuous in . Let these functions be continuous in and have continuous first Partial Derivatives and have continuous first Partial Derivatives  for for  ,..., ,...,  and and  , ..., , ...,  in in  . Let . Let  be in be in  . Then there existsa solution of (4) given by . Then there existsa solution of (4) given by
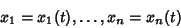 | (5) |
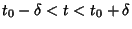 (where (where  ) satisfying the initial conditions ) satisfying the initial conditions
 | (6) |
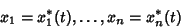 | (7) |
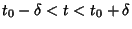 satisfying (6), then satisfying (6), then  for for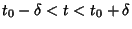 . Because every . Because every  th-order ODE can be expressed as a system of th-order ODE can be expressed as a system of  first-order differentialequations, this theorem also applies to the single first-order differentialequations, this theorem also applies to the single  th-order ODE. th-order ODE.
In general, an  th-order ODE has th-order ODE has  linearly independent solutions. Furthermore, any linear combination ofLinearly Independent Functions solutions is also a solution. linearly independent solutions. Furthermore, any linear combination ofLinearly Independent Functions solutions is also a solution.
An exact First-Order ODEs is one of the form
 | (8) |
 | (9) |
 | (10) |
 | (11) |
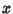 -dependent integrating factor. If -dependent integrating factor. If
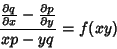 | (12) |
 -dependent integrating factor. If -dependent integrating factor. If
 | (13) |
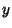 -dependent integrating factor. -dependent integrating factor.
Other special first-order types include cross multiple equations
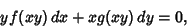 | (14) |
 | (15) |
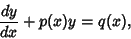 | (16) |
 | (17) |
Special classes of Second-Order ODEs include
 | (18) |
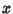 missing) and missing) and
 | (19) |
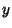 missing). A second-order linear homogeneous ODE missing). A second-order linear homogeneous ODE
 | (20) |
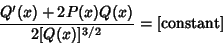 | (21) |
The undamped equation of Simple Harmonic Motion is
 | (22) |
 | (23) |
 | (24) |
Systems with Constant Coefficients are of the form
 | (25) |
The following are examples of important ordinary differential equations which commonly arise in problems ofmathematical physics.
Airy Differential Equation
 | (26) |
Bernoulli Differential Equation
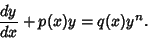 | (27) |
Bessel Differential Equation
 | (28) |
Chebyshev Differential Equation
 | (29) |
Confluent Hypergeometric Differential Equation
 | (30) |
Euler Differential Equation
 | (31) |
Hermite Differential Equation
 | (32) |
Hill's Differential Equation
 | (33) |
Hypergeometric Differential Equation
 | (34) |
Jacobi Differential Equation
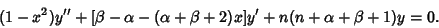 | (35) |
Laguerre Differential Equation
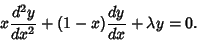 | (36) |
Lane-Emden Differential Equation
 | (37) |
Legendre Differential Equation
 | (38) |
Linear Constant Coefficients
 | (39) |
Malmstén's Differential Equation
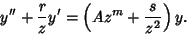 | (40) |
Riccati Differential Equation
 | (41) |
Riemann P-Differential Equation  | |  | (42) |
See also Adams' Method, Green's Function, Isocline, Laplace Transform, Leading OrderAnalysis, Majorant, Ordinary Differential Equation--First-Order,Ordinary Differential Equation--Second-Order, Partial Differential Equation,Relaxation Methods, Runge-Kutta Method, Simple Harmonic Motion
References
 Ordinary Differential Equations Ordinary Differential EquationsBoyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley, 1992. Braun, M. Differential Equations and Their Applications, 4th ed. New York: Springer-Verlag, 1993. Forsyth, A. R. Theory of Differential Equations, 6 vols. New York: Dover, 1959. Forsyth, A. R. A Treatise on Differential Equations. New York: Dover, 1997. Guterman, M. M. and Nitecki, Z. H. Differential Equations: A First Course, 3rd ed. Philadelphia, PA: Saunders, 1992. Ince, E. L. Ordinary Differential Equations. New York: Dover, 1956. Milne, W. E. Numerical Solution of Differential Equations. New York: Dover, 1970. Morse, P. M. and Feshbach, H. ``Ordinary Differential Equations.'' Ch. 5 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 492-675, 1953. Moulton, F. R. Differential Equations. New York: Dover, 1958. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Integration of Ordinary Differential Equations.'' Ch. 16 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 701-744, 1992. Simmons, G. F. Differential Equations, with Applications and Historical Notes, 2nd ed. New York: McGraw-Hill, 1991. Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.
|
![]() is an equation of the form
is an equation of the form![]() th-order ODE has
th-order ODE has ![]() linearly independent solutions. Furthermore, any linear combination ofLinearly Independent Functions solutions is also a solution.
linearly independent solutions. Furthermore, any linear combination ofLinearly Independent Functions solutions is also a solution.

![]() Ordinary Differential Equations
Ordinary Differential Equations