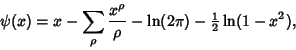| 释义 |
Mangoldt FunctionThe function defined by
 | (1) |
 is also given by [1, 2, ..., is also given by [1, 2, ..., 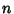 ]/[1, 2, ..., ]/[1, 2, ..., 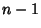 ], where ], where  denotes the LeastCommon Multiple. The first few values of denotes the LeastCommon Multiple. The first few values of  for for  , 2, ..., plotted above, are 1, 2, 3, 2, 5, 1, 7, 2, ...(Sloane's A014963). The Mangoldt function is related to the Riemann Zeta Function , 2, ..., plotted above, are 1, 2, 3, 2, 5, 1, 7, 2, ...(Sloane's A014963). The Mangoldt function is related to the Riemann Zeta Function 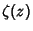 by by
 | (2) |
 . .
The Summatory Mangoldt function, illustrated above, is defined by
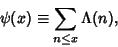 | (3) |
 is the Mangoldt Function. This has the explicit formula is the Mangoldt Function. This has the explicit formula
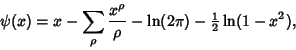 | (4) |
 of the Riemann Zeta Function of the Riemann Zeta Function  andinterpreted as andinterpreted as
 | (5) |
 | (6) |
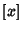 is the Nint function and is the Nint function and 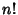 is a Factorial. is a Factorial.
Vallée Poussin's version of the Prime Number Theorem states that
 | (7) |
 (Davenport 1980, Vardi 1991). The Riemann Hypothesis is equivalent to (Davenport 1980, Vardi 1991). The Riemann Hypothesis is equivalent to
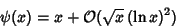 | (8) |
References
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, p. 110, 1980.Sloane, N. J. A. Sequence A014963in ``The On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 146-147, 152-153, and 249, 1991.
|