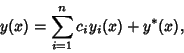| 释义 |
Ordinary Differential Equation--First-OrderGiven a first-order Ordinary Differential Equation
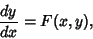 | (1) |
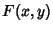 can be expressed using Separation of Variables as can be expressed using Separation of Variables as
 | (2) |
 | (3) |
 | (4) |
Any first-order ODE of the form
 | (5) |
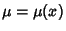 such that such that
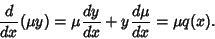 | (6) |
 yields yields
 | (7) |
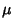 for arbitrary for arbitrary 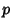 and and  . To accomplishthis, take . To accomplishthis, take
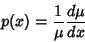 | (8) |
 | (9) |
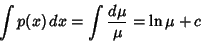 | (10) |
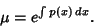 | (11) |
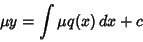 | (12) |
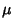 now a known function), which can be solved for now a known function), which can be solved for 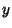 to obtain to obtain
 | (13) |
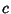 is an arbitrary constant of integration. is an arbitrary constant of integration.
Given an  th-order linear ODE with constant Coefficients th-order linear ODE with constant Coefficients
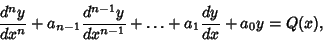 | (14) |
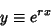 | (15) |
 to obtain the to obtain the  Complex Roots. Complex Roots.
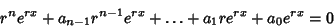 | (16) |
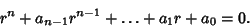 | (17) |
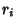 , ,
 | (18) |
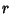 , the corresponding solution is , the corresponding solution is
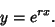 | (19) |
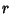 is repeated is repeated  times, the solutions are degenerate and the linearlyindependent solutions are times, the solutions are degenerate and the linearlyindependent solutions are
 | (20) |
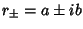 . For nonrepeatedComplex Roots, the solutions are . For nonrepeatedComplex Roots, the solutions are
 | (21) |
 times, the linearly independent solutionsare times, the linearly independent solutionsare
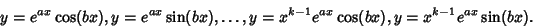 | (22) |
Linearly combining solutions of the appropriate types with arbitrary multiplicative constants then gives the completesolution. If initial conditions are specified, the constants can be explicitly determined. For example, consider thesixth-order linear ODE
 | (23) |
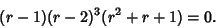 | (24) |
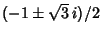 , so the solution is , so the solution is
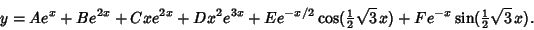 | (25) |
If the original equation is nonhomogeneous (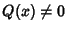 ), now find the particular solution ), now find the particular solution  by the method ofVariation of Parameters. The general solution is then by the method ofVariation of Parameters. The general solution is then
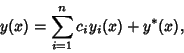 | (26) |
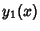 , ,  , ..., , ..., 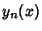 , and , and 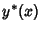 is the particularsolution.See also Integrating Factor, Ordinary Differential Equation--First-Order Exact, Separation of Variables, Variation of Parameters is the particularsolution.See also Integrating Factor, Ordinary Differential Equation--First-Order Exact, Separation of Variables, Variation of Parameters
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 440-445, 1985.
|
![]() th-order linear ODE with constant Coefficients
th-order linear ODE with constant Coefficients![]() ), now find the particular solution
), now find the particular solution ![]() by the method ofVariation of Parameters. The general solution is then
by the method ofVariation of Parameters. The general solution is then