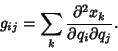| 释义 |
Metric TensorA Tensor, also called a Riemannian Metric, which is symmetric and Positive Definite. Very roughly, the metric tensor  is a function which tells how to compute the distance betweenany two points in a given Space. Its components can be viewed as multiplication factors which must be placed infront of the differential displacements is a function which tells how to compute the distance betweenany two points in a given Space. Its components can be viewed as multiplication factors which must be placed infront of the differential displacements  in a generalized Pythagorean Theorem in a generalized Pythagorean Theorem
 | (1) |
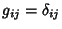 where where 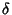 is the Kronecker Delta (which is 0 for is the Kronecker Delta (which is 0 for  and 1 for and 1 for  ), reproducing the usual form of the Pythagorean Theorem ), reproducing the usual form of the Pythagorean Theorem
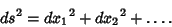 | (2) |
The metric tensor is defined abstractly as an Inner Product of every Tangent Space of a Manifold suchthat the Inner Product is a symmetric, nondegenerate, bilinear form on a Vector Space. This means that ittakes two Vectors  as arguments and produces a Real Number as arguments and produces a Real Number  such that such that
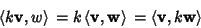 | (3) |
 | (4) |
 | (5) |
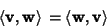 | (6) |
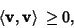 | (7) |
 . .
In coordinate Notation (with respect to the basis),
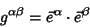 | (8) |
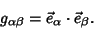 | (9) |
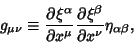 | (10) |
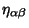 is the Minkowski Metric. This can also be written is the Minkowski Metric. This can also be written
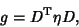 | (11) |
 | (14) |
 | (15) |
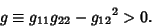 | (16) |
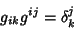 | (17) |
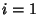 , ..., , ..., 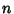 gives gives 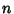 linear equations relating the linear equations relating the  quantities quantities  and and 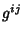 . Therefore, if . Therefore, if 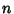 metrics are known, the others can be determined. metrics are known, the others can be determined.
In 2-space,
If 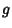 is symmetric, then is symmetric, then
In Euclidean Space (and all other symmetric Spaces),
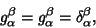 | (23) |
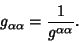 | (24) |
 between two parametric curves is given by between two parametric curves is given by
 | (25) |
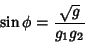 | (26) |
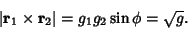 | (27) |
The Line Element can be written
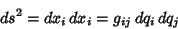 | (28) |
 | (29) |
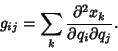 | (30) |
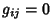 for for  , and the Line Element becomes (for 3-space) , and the Line Element becomes (for 3-space)
where 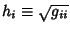 are called the Scale Factors.See also Curvilinear Coordinates, Discriminant (Metric), Lichnerowicz Conditions, Line Element,Metric, Metric Equivalence Problem, Minkowski Space, Scale Factor, Space are called the Scale Factors.See also Curvilinear Coordinates, Discriminant (Metric), Lichnerowicz Conditions, Line Element,Metric, Metric Equivalence Problem, Minkowski Space, Scale Factor, Space
|
![]() is a function which tells how to compute the distance betweenany two points in a given Space. Its components can be viewed as multiplication factors which must be placed infront of the differential displacements
is a function which tells how to compute the distance betweenany two points in a given Space. Its components can be viewed as multiplication factors which must be placed infront of the differential displacements ![]() in a generalized Pythagorean Theorem
in a generalized Pythagorean Theorem![]() as arguments and produces a Real Number
as arguments and produces a Real Number ![]() such that
such that