| 释义 |
Ordinary Differential Equation--First-Order ExactConsider a first-order ODE in the slightly different form
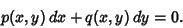 | (1) |
 | (2) |
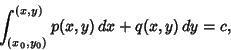 | (3) |
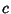 is a constant. is a constant.
A first-order ODE (1) is said to be inexact if
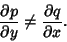 | (4) |
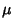 of (6) so that thenew equation of (6) so that thenew equation
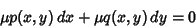 | (5) |
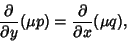 | (6) |
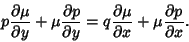 | (7) |
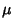 gives gives
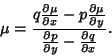 | (8) |
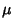 satisfying (8) can be found, then writing satisfying (8) can be found, then writing
in equation (5) then gives
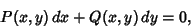 | (11) |
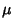 can be found include can be found include 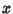 -dependent, -dependent,  -dependent, and -dependent, and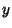 -dependent integrating factors. -dependent integrating factors.
Given an inexact first-order ODE, we can also look for an Integrating Factor 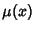 so that so that
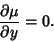 | (12) |
 and and 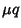 , the equation for a first-order nonexact ODE , the equation for a first-order nonexact ODE
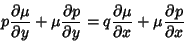 | (13) |
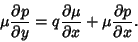 | (14) |
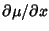 gives gives
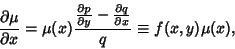 | (15) |
 | (16) |
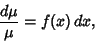 | (17) |
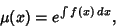 | (18) |
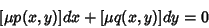 | (19) |
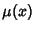 is now exact and can be solved as an exact ODE. is now exact and can be solved as an exact ODE.
Given in an exact first-order ODE, look for an Integrating Factor 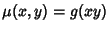 . Then . Then
 | (20) |
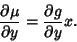 | (21) |
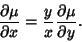 | (22) |
 and and 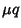 , the equation for a first-order nonexact ODE , the equation for a first-order nonexact ODE
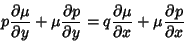 | (23) |
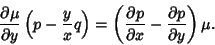 | (24) |
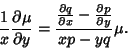 | (25) |
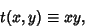 | (26) |
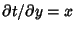 , so , so
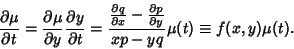 | (27) |
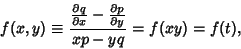 | (28) |
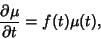 | (29) |
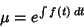 | (30) |
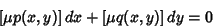 | (31) |
Given an inexact first-order ODE, assume there exists an integrating factor
 | (32) |
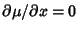 . For the equation to be exact in . For the equation to be exact in  and and 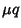 , equation (7) becomes , equation (7) becomes
 | (33) |
 | (34) |
 | (35) |
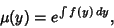 | (36) |
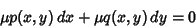 | (37) |
Given a first-order ODE of the form
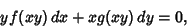 | (38) |
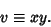 | (39) |
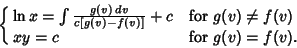 | (40) |
If
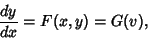 | (41) |
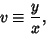 | (42) |
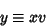 | (43) |
 | (44) |
 | (45) |
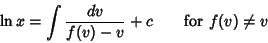 | (46) |
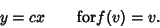 | (47) |
References
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, 1986.
|
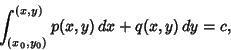
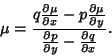
![]() so that
so that![]() . Then
. Then