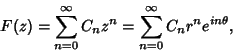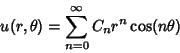| 释义 |
Abel's TheoremGiven a Taylor Series
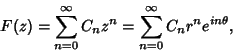 | (1) |
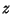 has been written in the polar form has been written in the polar form 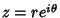 , examinethe Real and Imaginary Parts , examinethe Real and Imaginary Parts
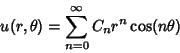 | (2) |
 | (3) |
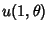 and and 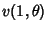 are Convergent, then are Convergent, then
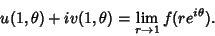 | (4) |
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 773, 1985.
|