| 释义 |
Descartes Total Angular DefectThe total angular defect is the sum of the Angular Defects over all Vertices of a Polyhedron, wherethe Angular Defect  at a given Vertex is the difference between the sum of faceangles and at a given Vertex is the difference between the sum of faceangles and  . For any convex Polyhedron, the Descartes total angular defect is . For any convex Polyhedron, the Descartes total angular defect is
 | (1) |
 | (2) |
A Polyhedron with  equivalent Verticesis called a Platonic Solid and can be assigned a Schläfli Symbol equivalent Verticesis called a Platonic Solid and can be assigned a Schläfli Symbol 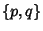 .It then satisfies .It then satisfies
 | (3) |
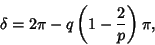 | (4) |
 | (5) |
|
![]() at a given Vertex is the difference between the sum of faceangles and
at a given Vertex is the difference between the sum of faceangles and ![]() . For any convex Polyhedron, the Descartes total angular defect is
. For any convex Polyhedron, the Descartes total angular defect is![]() equivalent Verticesis called a Platonic Solid and can be assigned a Schläfli Symbol
equivalent Verticesis called a Platonic Solid and can be assigned a Schläfli Symbol ![]() .It then satisfies
.It then satisfies