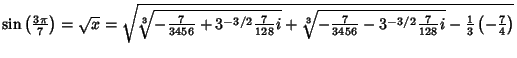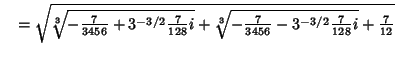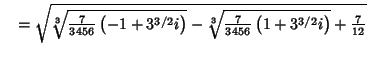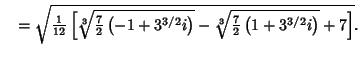| 释义 |
Trigonometry Values Pi/7Trigonometric functions of 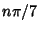 for for 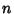 an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagonis not a Constructible Polygon. an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagonis not a Constructible Polygon.
However, exact expressions involving roots of complex numbers can still be derived using the trigonometric identity
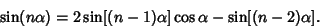 | (1) |
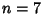 givesRewrite this using the identity givesRewrite this using the identity 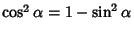 , , | |  | (3) |
Now, let  and and 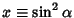 , then , then
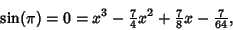 | (4) |
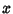 . The Roots are numerically found to be . The Roots are numerically found to be 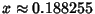 , ,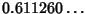 , , 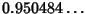 . But . But 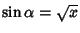 , so these Roots correspond to , so these Roots correspond to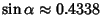 , ,  , , 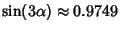 . By Newton'sRelation . By Newton'sRelation
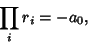 | (5) |
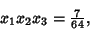 | (6) |
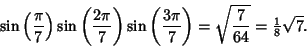 | (7) |
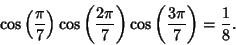 | (8) |
The Discriminant is then
so there are three distinct Real Roots. Finding the first one,
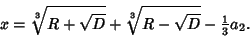 | (12) |
Writing
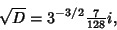 | (13) |
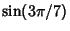 ,See also Heptagon ,See also Heptagon
|
![]() for
for ![]() an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagonis not a Constructible Polygon.
an integer cannot be expressed in terms of sums, products, and finite rootextractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagonis not a Constructible Polygon.