| 释义 |
Compound InterestLet 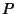 be the Principal (initial investment), be the Principal (initial investment),  be the annual compounded rate, be the annual compounded rate, 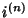 the ``nominal rate,'' the ``nominal rate,'' be the number of times Interest is compounded per year (i.e., the year is divided into be the number of times Interest is compounded per year (i.e., the year is divided into  ConversionPeriods), and ConversionPeriods), and 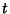 be the number of years (the ``term''). The Interest rate per ConversionPeriod is then be the number of years (the ``term''). The Interest rate per ConversionPeriod is then
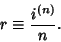 | (1) |
 times at an annual rate of times at an annual rate of  (where, for example, 10% corresponds to (where, for example, 10% corresponds to 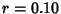 ), then theeffective rate over ), then theeffective rate over  the time (what an investor would earn if he did not redeposit his interest after each compounding)is the time (what an investor would earn if he did not redeposit his interest after each compounding)is
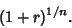 | (2) |
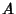 after a time after a time 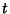 when interest is re-invested is then when interest is re-invested is then
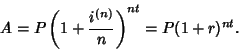 | (3) |
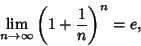 | (4) |
The time required for a given Principal to double (assuming  Conversion Period) is given by solving Conversion Period) is given by solving
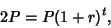 | (5) |
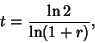 | (6) |
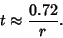 | (7) |
References
Kellison, S. G. The Theory of Interest, 2nd ed. Burr Ridge, IL: Richard D. Irwin, pp. 14-16, 1991.Milanfar, P. ``A Persian Folk Method of Figuring Interest.'' Math. Mag. 69, 376, 1996.
|
![]() be the Principal (initial investment),
be the Principal (initial investment), ![]() be the annual compounded rate,
be the annual compounded rate, ![]() the ``nominal rate,''
the ``nominal rate,''![]() be the number of times Interest is compounded per year (i.e., the year is divided into
be the number of times Interest is compounded per year (i.e., the year is divided into ![]() ConversionPeriods), and
ConversionPeriods), and ![]() be the number of years (the ``term''). The Interest rate per ConversionPeriod is then
be the number of years (the ``term''). The Interest rate per ConversionPeriod is then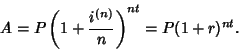
![]() Conversion Period) is given by solving
Conversion Period) is given by solving