Uniform Convergence
A Series 
is uniformly convergent to 
for a set 
of values of 
if, for each
, an Integer 
can be found such that
 | (1) |
and all 
. To test for uniform convergence, use Abel's Uniform Convergence Test or theWeierstraß M-Test. If individual terms 
of a uniformly converging series arecontinuous, then- 1. The series sumis continuous,
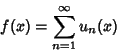
(2) - 2. The series may be integrated term by termand
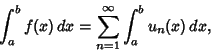
(3) - 3. The series may be differentiated term by term
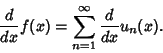
(4)
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 299-301, 1985.
- Peano-Gosper Curve
- Peano's Axioms
- Peano Surface
- Pear Curve
- Pearls of Sluze
- Pear-Shaped Curve
- Pearson-Cunningham Function
- Pearson Kurtosis
- Pearson Mode Skewness
- Pearson's Correlation
- Pearson's Function
- Pearson Skewness
- Pearson's Skewness Coefficients
- Pearson System
- Pearson Type III Distribution
- Peaucellier Cell
- Peaucellier Inversor
- Peaucellier's Linkage
- Pedal
- Pedal Circle
- Pedal Coordinates
- Pedal Curve
- Pedal Line
- Pedal Point
- Pedal Triangle