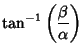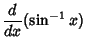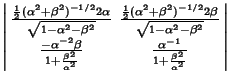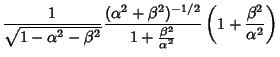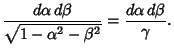| 释义 |
Direction CosineLet  be the Angle between be the Angle between 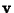 and and 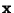 , ,  the Angle between the Angle between 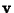 and and 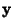 , and , and  the Angle between the Angle between 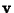 and and 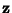 . Then the direction cosines are equivalent to the . Then the direction cosines are equivalent to the 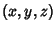 coordinatesof a Unit Vector coordinatesof a Unit Vector 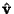 , ,
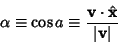 | (1) |
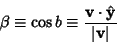 | (2) |
 | (3) |
 | (4) |
The Jacobian is
 | (8) |
so
Direction cosines can also be defined between two sets of Cartesian Coordinates,
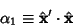 | (13) |
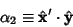 | (14) |
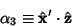 | (15) |
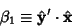 | (16) |
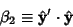 | (17) |
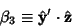 | (18) |
 | (19) |
 | (20) |
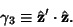 | (21) |
and
Projections of the primed coordinates onto the unprimed coordinates yield
and
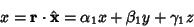 | (31) |
 | (32) |
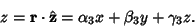 | (33) |
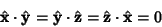 | (34) |
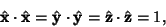 | (35) |
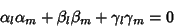 | (36) |
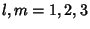 and and 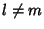 , and , and
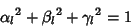 | (37) |
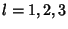 . These two identities may be combined into the single identity . These two identities may be combined into the single identity
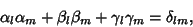 | (38) |
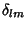 is the Kronecker Delta. is the Kronecker Delta.
|
![]() be the Angle between
be the Angle between ![]() and
and ![]() ,
, ![]() the Angle between
the Angle between ![]() and
and ![]() , and
, and ![]() the Angle between
the Angle between ![]() and
and ![]() . Then the direction cosines are equivalent to the
. Then the direction cosines are equivalent to the ![]() coordinatesof a Unit Vector
coordinatesof a Unit Vector ![]() ,
,