“Discriminant (Quadratic Curve)”的概念、定义、习题解题方法及翻译-数学辞典

单词

Discriminant (Quadratic Curve)

释义

Discriminant (Quadratic Curve)

Given a general Quadratic Curve

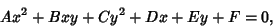(1)

the quantity

is known as the discriminant, where

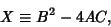(2)

and is invariant under Rotation. Using the Coefficients from QuadraticEquations for a rotation by an angle


			(3)
			(4)

			(5)

Now let

			(6)
			(7)
			(8)

and use

			(9)
			(10)

to rewrite the primed variables

			(11)

			(12)
			(13)

From (11) and (13), it follows that

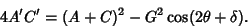(14)

Combining with (12) yields, for an arbitrary




			(15)

which is therefore invariant under rotation. This invariant therefore provides a useful shortcut to determining theshape represented by a Quadratic Curve. Choosing

to make

(see Quadratic Equation), thecurve takes on the form

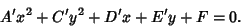(16)

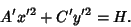Completing the Square and defining new variables gives

(17)

Without loss of generality, take the sign of

to be positive. The discriminant is

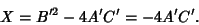(18)

Now, if

, then

and

both have the same sign, and the equation has the general form of an Ellipse (if

and

are positive). If

, then

and

have opposite signs, and the equation hasthe general form of a Hyperbola. If

, then either

is zero, and the equation has thegeneral form of a Parabola (if the Nonzero

is positive). Since the discriminant is invariant, theseconclusions will also hold for an arbitrary choice of

, so they also hold when

is replaced by theoriginal

. The general result is

: 1. If , the equation represents an Ellipse, a Circle (degenerate Ellipse),a Point (degenerate Circle), or has no graph.
: 2. If , the equation represents a Hyperbola or pair of intersecting lines (degenerateHyperbola).
: 3. If , the equation represents a Parabola, a Line (degenerate Parabola),a pair of Parallel lines (degenerate Parabola), or has no graph.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。