Divisibility Tests
Write a positive decimal integer ![]() out digit by digit in the form
out digit by digit in the form ![]() . The following rules thendetermine if
. The following rules thendetermine if ![]() is divisible by another number by examining the Congruence properties of its digits.
is divisible by another number by examining the Congruence properties of its digits.
- 2.
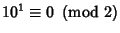 , so
, so  for
for  . Therefore, if the last digit
. Therefore, if the last digit 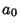 is divisible by 2(i.e., is Even), then so is
is divisible by 2(i.e., is Even), then so is  .
. - 3.
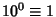 ,
,  ,
,  , ...,
, ..., 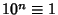 (mod 3). Therefore, if
(mod 3). Therefore, if 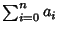 is divisible by 3, so is
is divisible by 3, so is  .
. - 4.
 ,
, 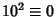 , ...
, ...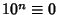 (mod 4). So if the last two digits are divisible by 4, morespecifically if
(mod 4). So if the last two digits are divisible by 4, morespecifically if 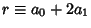 is, then so is
is, then so is  .
. - 5.
 , so
, so 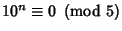 for
for  . Therefore, if the last digit
. Therefore, if the last digit 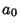 is divisible by 5 (i.e.,is 5 or 0), then so is
is divisible by 5 (i.e.,is 5 or 0), then so is 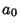 .
. - 6.
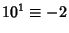 ,
,  , ...,
, ..., 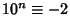 (mod 6). Therefore, if
(mod 6). Therefore, if 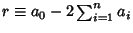 isdivisible by 6, so is
isdivisible by 6, so is  . A simpler rule states that if
. A simpler rule states that if  is divisible by 3 and is Even, then
is divisible by 3 and is Even, then  is also divisible by 6.
is also divisible by 6. - 7.
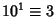 ,
, 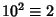 ,
,  ,
, 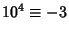 ,
,  ,
, 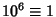 (mod 7), and thesequence then repeats. Therefore, if
(mod 7), and thesequence then repeats. Therefore, if 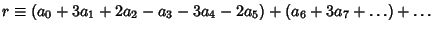 is divisible by 7, sois
is divisible by 7, sois  .
. - 8.
 ,
, 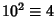 ,
,  , ...,
, ..., 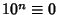 (mod 8). Therefore, if the last three digitsare divisible by 8, more specifically if
(mod 8). Therefore, if the last three digitsare divisible by 8, more specifically if  is, then so is
is, then so is  .
. - 9.
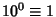 ,
,  ,
,  , ...,
, ..., 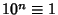 (mod 9). Therefore, if
(mod 9). Therefore, if 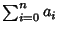 is divisible by 9,so is
is divisible by 9,so is  .
. - 10.
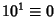 (mod 10), so if the last digit is 0, then
(mod 10), so if the last digit is 0, then  is divisible by 10.
is divisible by 10. - 11.
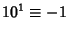 ,
,  ,
,  ,
, 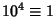 , ... (mod 11). Therefore, if
, ... (mod 11). Therefore, if 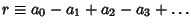 is divisible by 11, then so is
is divisible by 11, then so is  .
. - 12.
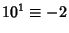 ,
, 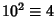 ,
,  , ... (mod 12). Therefore, if
, ... (mod 12). Therefore, if  is divisible by 12, then so is
is divisible by 12, then so is  . Divisibility by 12 can also be checked by seeing if
. Divisibility by 12 can also be checked by seeing if  is divisible by 3 and4.
is divisible by 3 and4. - 13.
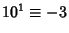 ,
, 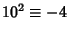 ,
,  ,
, 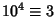 ,
,  ,
, 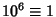 (mod 13), and thepattern repeats. Therefore, if
(mod 13), and thepattern repeats. Therefore, if  is divisible by 13, so is
is divisible by 13, so is .
.
References
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 337-346, 1952. Gardner, M. Ch. 14 in The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University Press, 1991.
- Measurable Function
- Measurable Set
- Measurable Space
- Measure
- Measure Algebra
- Measure Polytope
- Measure-Preserving Transformation
- Measure Space
- Measure Theory
- Mechanical Quadrature
- Mecon
- Medial Axis
- Medial Deltoidal Hexecontahedron
- Medial Disdyakis Triacontahedron
- Medial Hexagonal Hexecontahedron
- Medial Icosacronic Hexecontahedron
- Medial Inverted Pentagonal Hexecontahedron
- Medial Pentagonal Hexecontahedron
- Medial Rhombic Triacontahedron
- Medial Triambic Icosahedron
- Medial Triangle
- Medial Triangle Locus Theorem
- Median Point
- Median (Statistics)
- Mediant