| 释义 |
DivisorA divisor of a number 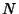 is a number is a number  which Divides which Divides 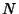 , also called a Factor. The total number ofdivisors for a given number , also called a Factor. The total number ofdivisors for a given number 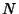 can be found as follows. Write a number in terms of its Prime Factorization can be found as follows. Write a number in terms of its Prime Factorization
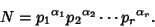 | (1) |
 of of 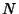 , , 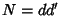 where where
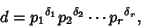 | (2) |
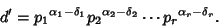 | (3) |
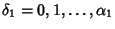 , so there are , so there are 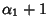 possible values. Similarly, for possible values. Similarly, for 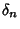 , there are , there are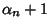 possible values, so the total number of divisors possible values, so the total number of divisors 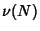 of of 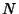 is given by is given by
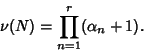 | (4) |
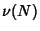 is also sometimes denoted is also sometimes denoted  or or  . The product of divisors can be found by writingthe number . The product of divisors can be found by writingthe number 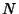 in terms of all possible products in terms of all possible products
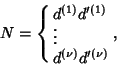 | (5) |
and
 | (7) |
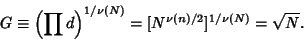 | (8) |
 with with  and and  . For any divisor . For any divisor  of of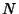 , ,  , where , where 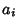 is a divisor of is a divisor of  and and 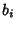 is a divisor of is a divisor of  . The divisors of . The divisors of  are 1, are 1, 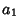 , ,  ,..., and ,..., and  . The divisors of . The divisors of  are 1, are 1, 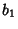 , , 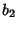 , ..., , ...,  . The sums of the divisors are then . The sums of the divisors are then
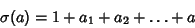 | (9) |
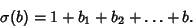 | (10) |
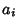 , ,
 | (11) |
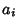 , ,
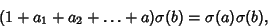 | (12) |
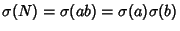 . Splitting . Splitting  and and  into prime factors, into prime factors,
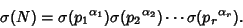 | (13) |
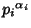 , the divisors are 1, , the divisors are 1,  , ,  , ..., , ..., 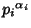 , so , so
 | (14) |
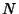 , therefore, , therefore,
 | (15) |
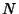 a Prime, (15) simplifies to a Prime, (15) simplifies to
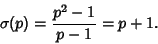 | (16) |
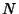 a Power of two, (15) simplifies to a Power of two, (15) simplifies to
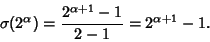 | (17) |
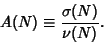 | (18) |
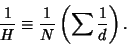 | (19) |
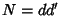 , so , so  and and
 | (20) |
 | (21) |
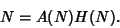 | (22) |
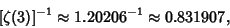 | (23) |
 is Apéry's Constant. is Apéry's Constant.
Let  be the number of elements in the greatest subset of be the number of elements in the greatest subset of 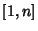 such that none of its elements are divisible by two others. For such that none of its elements are divisible by two others. For  sufficiently large, sufficiently large,
 | (24) |
References
Guy, R. K. ``Solutions of 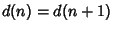 .'' §B18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 73-75, 1994. .'' §B18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 73-75, 1994.Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 43, 1983. Lebensold, K. ``A Divisibility Problem.'' Studies Appl. Math. 56, 291-294, 1976/1977.
|
![]() is a number
is a number ![]() which Divides
which Divides ![]() , also called a Factor. The total number ofdivisors for a given number
, also called a Factor. The total number ofdivisors for a given number ![]() can be found as follows. Write a number in terms of its Prime Factorization
can be found as follows. Write a number in terms of its Prime Factorization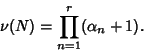
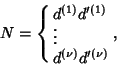
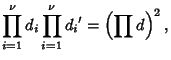

![]() be the number of elements in the greatest subset of
be the number of elements in the greatest subset of ![]() such that none of its elements are divisible by two others. For
such that none of its elements are divisible by two others. For ![]() sufficiently large,
sufficiently large,![]() .'' §B18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 73-75, 1994.
.'' §B18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 73-75, 1994.