| 释义 |
Whittaker FunctionSolutions to the Whittaker Differential Equation. The linearly independent solutions are
 | (1) |
and 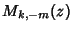 , where , where 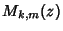 is a Confluent Hypergeometric Function. In terms of Confluent Hypergeometric Functions, the Whittaker functions are is a Confluent Hypergeometric Function. In terms of Confluent Hypergeometric Functions, the Whittaker functions are
 | (2) |
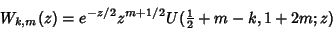 | (3) |
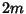 is an Integer, so Whittaker functions are often defined instead. The Whittaker functions are related to theParabolic Cylinder Functions. When is an Integer, so Whittaker functions are often defined instead. The Whittaker functions are related to theParabolic Cylinder Functions. When 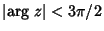 and and 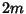 is not anInteger, is not anInteger,
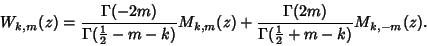 | (4) |
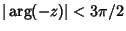 and and 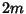 is not an Integer, is not an Integer,
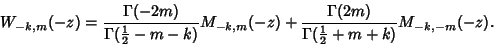 | (5) |
 | (6) |
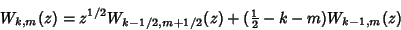 | (7) |
 | (8) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Confluent Hypergeometric Functions.'' Ch. 13 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 503-515, 1972.Iyanaga, S. and Kawada, Y. (Eds.). ``Whittaker Functions.'' Appendix A, Table 19.II in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1469-1471, 1980. Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
|
![]() , where
, where ![]() is a Confluent Hypergeometric Function. In terms of Confluent Hypergeometric Functions, the Whittaker functions are
is a Confluent Hypergeometric Function. In terms of Confluent Hypergeometric Functions, the Whittaker functions are