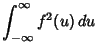| 释义 |
AutocorrelationThe autocorrelation function is defined by
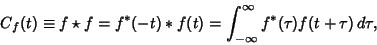 | (1) |
 denotes Convolution and denotes Convolution and  denotes Cross-Correlation. A finite autocorrelation is given by denotes Cross-Correlation. A finite autocorrelation is given by
If 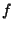 is a Real Function, is a Real Function,
 | (4) |
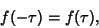 | (5) |
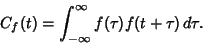 | (6) |
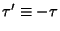 , so , so 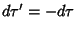 , then , then
The autocorrelation discards phase information, returning only the Power. It is therefore not reversible.
There is also a somewhat surprising and extremely important relationship between the autocorrelation and the FourierTransform known as the Wiener-Khintchine Theorem. Let 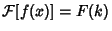 , and , and 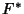 denote the ComplexConjugate of denote the ComplexConjugate of 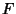 , then the Fourier Transform of the Absolute Square of , then the Fourier Transform of the Absolute Square of 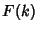 is given by is given by
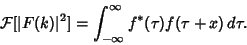 | (8) |
The autocorrelation is a Hermitian Operator since 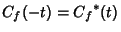 . .  is Maximum atthe Origin. In other words, is Maximum atthe Origin. In other words,
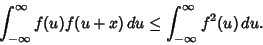 | (9) |
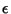 be a Real Number. Then be a Real Number. Then
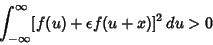 | (10) |
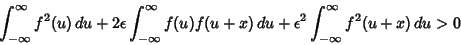 | (11) |
 | (12) |
Define
Then plugging into above, we have 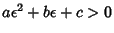 . This Quadratic Equation does not have any Real Root, so . This Quadratic Equation does not have any Real Root, so 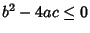 , i.e., , i.e., 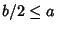 . It follows that . It follows that
 | (15) |
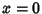 . This proves that . This proves that 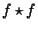 is Maximum at the Origin.See also Convolution, Cross-Correlation, Quantization Efficiency, Wiener-Khintchine Theorem is Maximum at the Origin.See also Convolution, Cross-Correlation, Quantization Efficiency, Wiener-Khintchine Theorem
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Correlation and Autocorrelation Using the FFT.'' §13.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 538-539, 1992. |
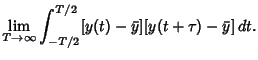
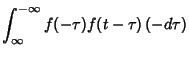

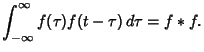
![]() , and
, and ![]() denote the ComplexConjugate of
denote the ComplexConjugate of ![]() , then the Fourier Transform of the Absolute Square of
, then the Fourier Transform of the Absolute Square of ![]() is given by
is given by![]() .
. ![]() is Maximum atthe Origin. In other words,
is Maximum atthe Origin. In other words,