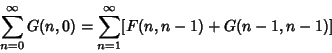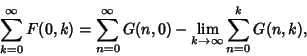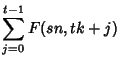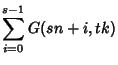| 释义 |
Wilf-Zeilberger PairA pair of Closed Form functions 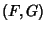 is said to be a Wilf-Zeilberger pair if is said to be a Wilf-Zeilberger pair if
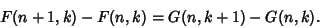 | (1) |
Wilf-Zeilberger pairs are very useful in proving Hypergeometric Identities of the form
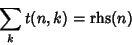 | (2) |
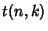 vanishes for all vanishes for all 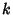 outside some finite interval. Now divide by the right-hand side to obtain outside some finite interval. Now divide by the right-hand side to obtain
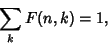 | (3) |
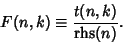 | (4) |
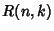 provided by Zeilberger's Algorithm, define provided by Zeilberger's Algorithm, define
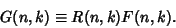 | (5) |
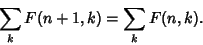 | (6) |
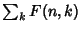 is independent of is independent of 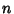 , and so must be a constant. If , and so must be a constant. If 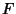 is properly normalized, thenit will be true that is properly normalized, thenit will be true that  . .
For example, consider the Binomial Coefficient identity
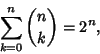 | (7) |
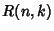 returned by Zeilberger's Algorithm is returned by Zeilberger's Algorithm is
 | (8) |
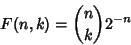 | (9) |
Taking
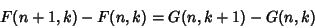 | (11) |
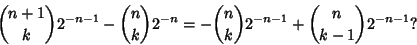 | (12) |
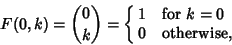 | (13) |
 (Petkovsek et al. 1996, pp. 25-27). (Petkovsek et al. 1996, pp. 25-27).
For any Wilf-Zeilberger pair 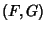 , ,
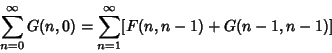 | (14) |
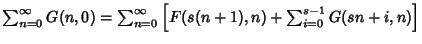 | | 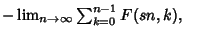 | (15) |
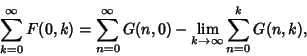 | (16) |
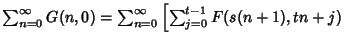 | |  | (17) |
where
(Amdeberhan and Zeilberger 1997). The latter identity has been used to compute Apéry's Constant to a large number of decimal places (Plouffe).See also Apéry's Constant, Convergence Improvement, Zeilberger's Algorithm
References
Amdeberhan, T. and Zeilberger, D. ``Hypergeometric Series Acceleration via the WZ Method.'' Electronic J. Combinatorics 4, No. 2, R3, 1-3, 1997.http://www.combinatorics.org/Volume_4/wilftoc.html#R03. Also available at http://www.math.temple.edu/~zeilberg/mamarim/mamarimhtml/accel.html.Cipra, B. A. ``How the Grinch Stole Mathematics.'' Science 245, 595, 1989. Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. ``The WZ Phenomenon.'' Ch. 7 in A=B. Wellesley, MA: A. K. Peters, pp. 121-140, 1996. Wilf, H. S. and Zeilberger, D. ``Rational Functions Certify Combinatorial Identities.'' J. Amer. Math. Soc. 3, 147-158, 1990. Zeilberger, D. ``The Method of Creative Telescoping.'' J. Symb. Comput. 11, 195-204, 1991. Zeilberger, D. ``Closed Form (Pun Intended!).'' Contemporary Math. 143, 579-607, 1993.
|
![]() is said to be a Wilf-Zeilberger pair if
is said to be a Wilf-Zeilberger pair if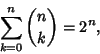
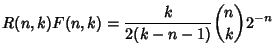
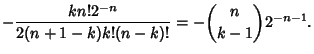
![]() ,
,