Eilenberg-Steenrod Axioms
A family of Functors ![]() from the Category of pairs of TopologicalSpaces and continuous maps, to the Category of Abelian Groups and grouphomomorphisms satisfies the Eilenberg-Steenrod axioms if the following conditions hold.
from the Category of pairs of TopologicalSpaces and continuous maps, to the Category of Abelian Groups and grouphomomorphisms satisfies the Eilenberg-Steenrod axioms if the following conditions hold.
- 1. Long Exact Sequence of a Pair Axiom. For every pair
 , there is a natural long exact sequence where the Map
, there is a natural long exact sequence where the Map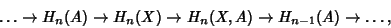
(1)  is induced by the Inclusion Map
is induced by the Inclusion Map  and
and  is induced bythe Inclusion Map
is induced bythe Inclusion Map  . The Map
. The Map  is called the Boundary Map.
is called the Boundary Map. - 2. Homotopy Axiom. If
 is homotopic to
is homotopic to  , then their InducedMaps
, then their InducedMaps  and
and  are the same.
are the same. - 3. Excision Axiom. If
 is a Space with Subspaces
is a Space with Subspaces  and
and  such that theClosure of
such that theClosure of  is contained in the interior of
is contained in the interior of  , then the Inclusion Map
, then the Inclusion Map  inducesan isomorphism
inducesan isomorphism  .
. - 4. Dimension Axiom. Let
 be a single point space.
be a single point space.  unless
unless  , in which case
, in which case  where
where  are some Groups. The
are some Groups. The  are called the Coefficients of the Homology theory
are called the Coefficients of the Homology theory  .
.
These are the axioms for a generalized homology theory. For a cohomology theory, instead of requiring that ![]() be aFunctor, it is required to be a co-functor (meaning the Induced Map points in the opposite direction). Withthat modification, the axioms are essentially the same (except that all the induced maps point backwards).
be aFunctor, it is required to be a co-functor (meaning the Induced Map points in the opposite direction). Withthat modification, the axioms are essentially the same (except that all the induced maps point backwards).
- Elliptic Plane
- Elliptic Point
- Elliptic Pseudoprime
- Elliptic Rotation
- Elliptic Theta Function
- Elliptic Torus
- Elliptic Umbilic Catastrophe
- Ellison-Mendès-France Constant
- Elongated Cupola
- Elongated Dipyramid
- Elongated Dodecahedron
- Elongated Gyrobicupola
- Elongated Gyrocupolarotunda
- Elongated Orthobicupola
- Elongated Orthobirotunda
- Elongated Orthocupolarotunda
- Elongated Pentagonal Cupola
- Elongated Pentagonal Dipyramid
- Elongated Pentagonal Gyrobicupola
- Elongated Pentagonal Gyrobirotunda
- Elongated Pentagonal Gyrocupolarotunda
- Elongated Pentagonal Orthobicupola
- Elongated Pentagonal Orthobirotunda
- Elongated Pentagonal Orthocupolarotunda
- Elongated Pentagonal Pyramid