| 释义 |
Elliptic Integral of the Second KindLet the Modulus  satisfy satisfy  . (This may also be written in terms ofthe Parameter . (This may also be written in terms ofthe Parameter  or Modular Angle or Modular Angle  .) The incomplete elliptic integralof the second kind is then defined as .) The incomplete elliptic integralof the second kind is then defined as
 | (1) |
 with with  gives gives
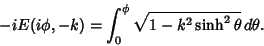 | (2) |
so the elliptic integral can also be written as
The complete elliptic integral of the second kind, illustrated above as a function of the Parameter  ,is defined by ,is defined by
where  is the Hypergeometric Function and is the Hypergeometric Function and  is a Jacobi Elliptic Function. The complete elliptic integral of the second kind satisfies the Legendre Relation is a Jacobi Elliptic Function. The complete elliptic integral of the second kind satisfies the Legendre Relation
 | (10) |
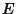 and and  are complete Elliptic Integrals of the First and second kinds,and are complete Elliptic Integrals of the First and second kinds,and 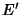 and and  are the complementary integrals. The Derivative is are the complementary integrals. The Derivative is
 | (11) |
 is a singular value (i.e., is a singular value (i.e.,
 | (12) |
 is the Elliptic Lambda Function), and is the Elliptic Lambda Function), and 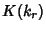 and the Elliptic Alpha Function and the Elliptic Alpha Function  arealso known, then arealso known, then
 | (13) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Elliptic Integrals.'' Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 587-607, 1972.Spanier, J. and Oldham, K. B. ``The Complete Elliptic Integrals  and and  '' and ``The Incomplete Elliptic Integrals '' and ``The Incomplete Elliptic Integrals  and and  .'' Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987. .'' Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987. Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990. |
![]() satisfy
satisfy ![]() . (This may also be written in terms ofthe Parameter
. (This may also be written in terms ofthe Parameter ![]() or Modular Angle
or Modular Angle ![]() .) The incomplete elliptic integralof the second kind is then defined as
.) The incomplete elliptic integralof the second kind is then defined as


![]() ,is defined by
,is defined by

![]() and
and ![]() '' and ``The Incomplete Elliptic Integrals
'' and ``The Incomplete Elliptic Integrals ![]() and
and ![]() .'' Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.
.'' Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.