| 释义 |
Error PropagationGiven a Formula 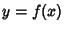 with an Absolute Error in with an Absolute Error in  of of 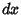 , the Absolute Error is , the Absolute Error is 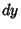 . TheRelative Error is . TheRelative Error is 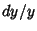 . If . If 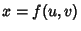 , then , then
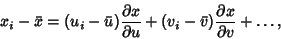 | (1) |
The definitions of Variance and Covariance then give
so
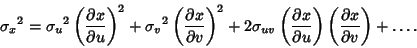 | (6) |
 and and  are uncorrelated, then are uncorrelated, then 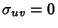 so so
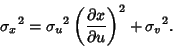 | (7) |
Now consider addition of quantities with errors.For  , , 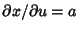 and and 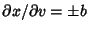 , so , so
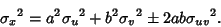 | (8) |
For division of quantities with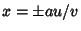 , , 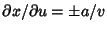 and and  , so , so
 | (9) |
For exponentiation of quantities with
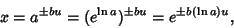 | (11) |
 | (12) |
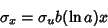 | (13) |
 | (14) |
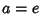 , then , then
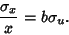 | (15) |
For Logarithms of quantities with 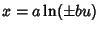 , , 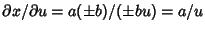 , so , so
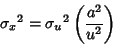 | (16) |
 | (17) |
For multiplication with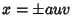 , , 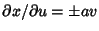 and and  , so , so
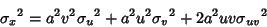 | (18) |
For Powers,with 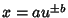 , ,  , so , so
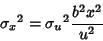 | (20) |
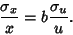 | (21) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.Bevington, P. R. Data Reduction and Error Analysis for the Physical Sciences. New York: McGraw-Hill, pp. 58-64, 1969. |
![]() with an Absolute Error in
with an Absolute Error in ![]() of
of ![]() , the Absolute Error is
, the Absolute Error is ![]() . TheRelative Error is
. TheRelative Error is ![]() . If
. If ![]() , then
, then

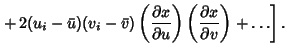
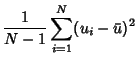
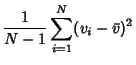
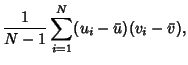
![]() ,
, ![]() and
and ![]() , so
, so![]() ,
, ![]() and
and ![]() , so
, so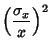
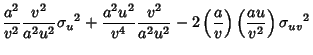
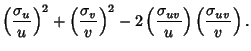
![]() ,
, ![]() , so
, so![]() ,
, ![]() and
and ![]() , so
, so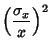


![]() ,
, ![]() , so
, so